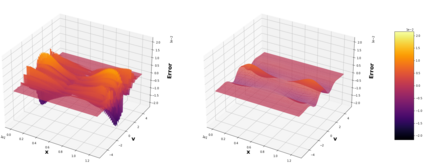
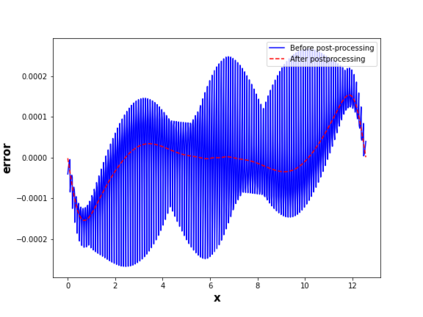
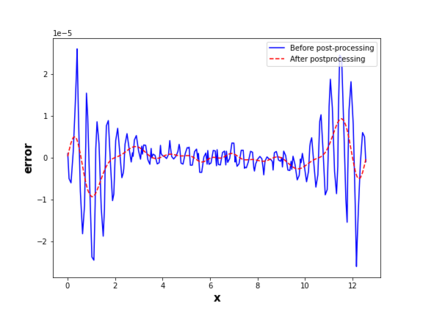
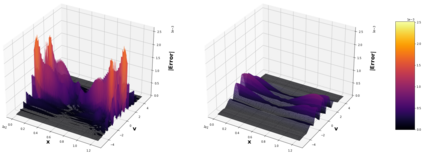
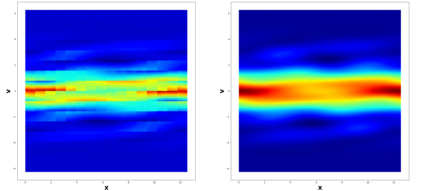
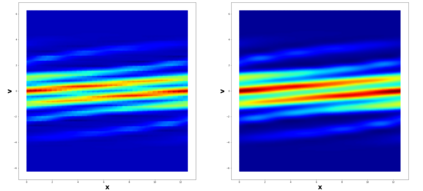
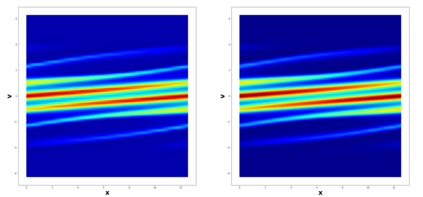
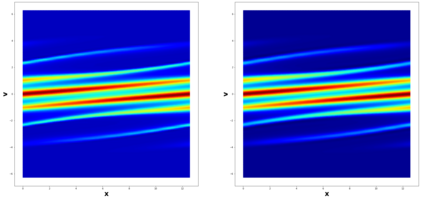
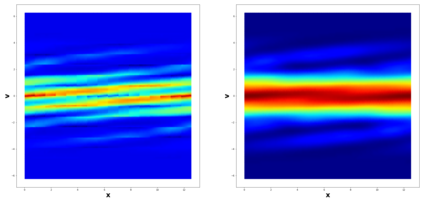
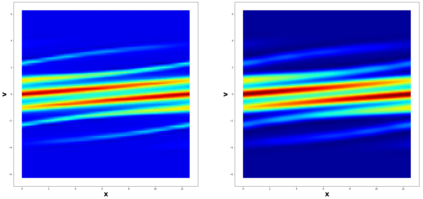
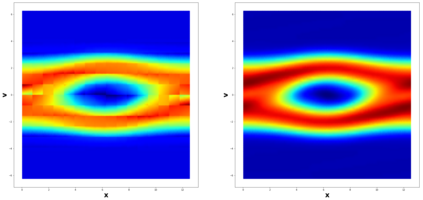
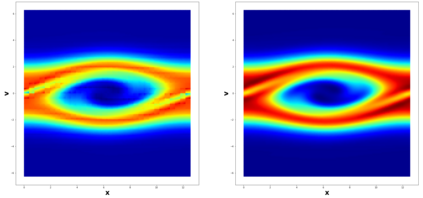
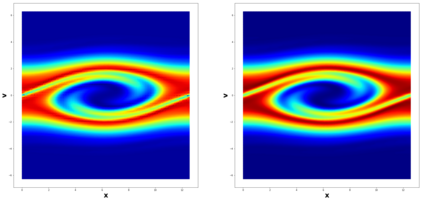
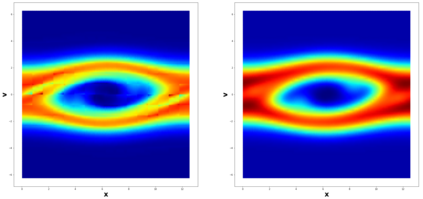
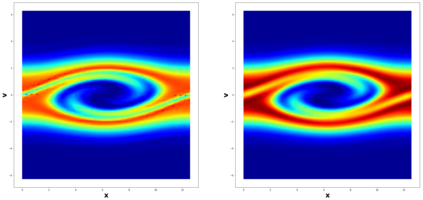
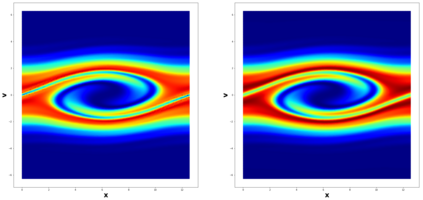
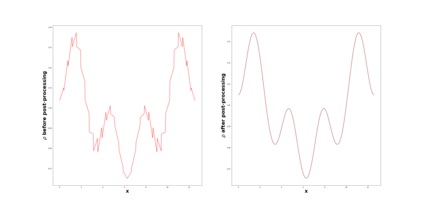
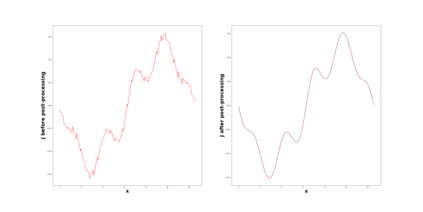
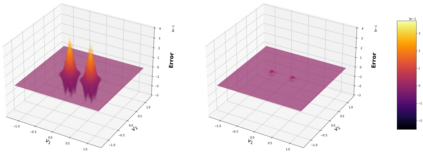
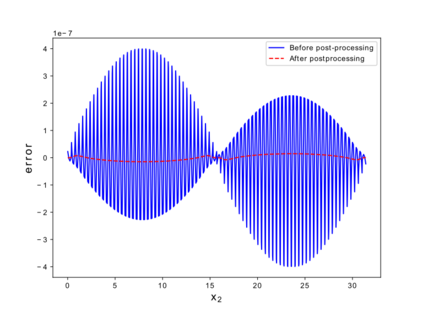
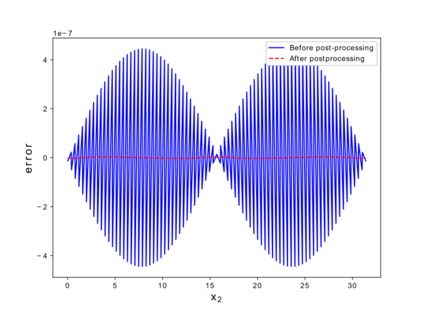
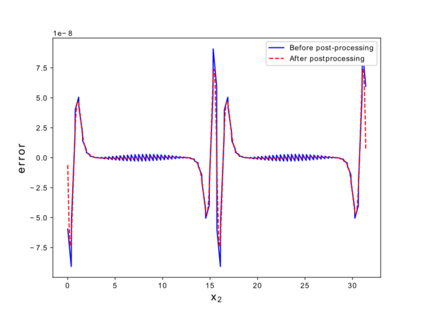
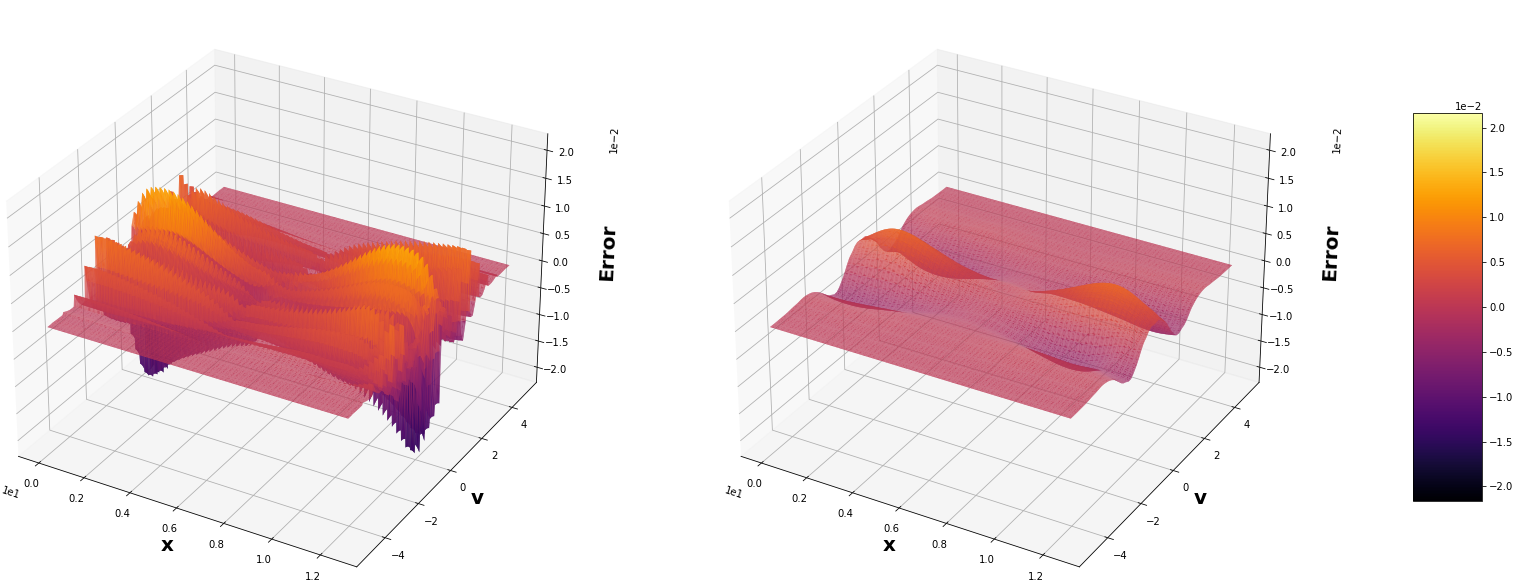
This paper considers the discontinuous Galerkin (DG) methods for solving the Vlasov-Maxwell (VM) system, a fundamental model for collisionless magnetized plasma. The DG methods provide accurate numerical description with conservation and stability properties. However, to resolve the high dimensional probability distribution function, the computational cost is the main bottleneck even for modern-day supercomputers. This work studies the applicability of a post-processing technique to the DG solution to enhance its accuracy and resolution for the VM system. In particular, we prove the superconvergence of order $(2k+\frac{1}{2})$ in the negative order norm for the probability distribution function and the electromagnetic fields when piecewise polynomial degree $k$ is used. Numerical tests including Landau damping, two-stream instability and streaming Weibel instabilities are considered showing the performance of the post-processor.
翻译:本文考虑了用于解决Vlasov-Maxwell(VM)系统(VM)的不连续的Galerkin(DG)方法,这是不碰撞磁性等离子体的基本模型。DG方法提供了保护和稳定性特性的精确数字描述。然而,为了解决高维概率分布函数,计算成本甚至对现代超级计算机来说也是主要的瓶颈。这项工作研究后处理技术对DG解决方案的适用性,以提高VM系统的精确度和分辨率。特别是,我们证明,在负顺序规范中,以$(2k ⁇ frac{1 ⁇ 2}为单位,在使用小巧聚米度时,概率分布函数和电磁场的超相趋同值。包括Landau悬崖、双流不稳定和流动 Weibel 不稳定性能在内的数字测试被视为显示后处理器的性能。