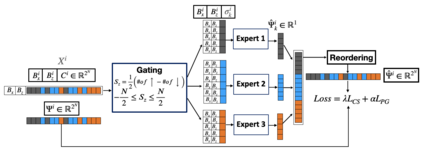
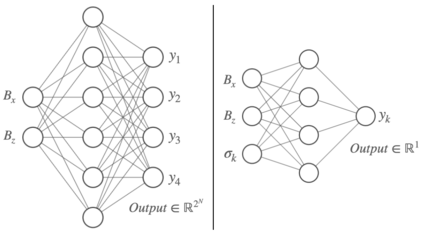
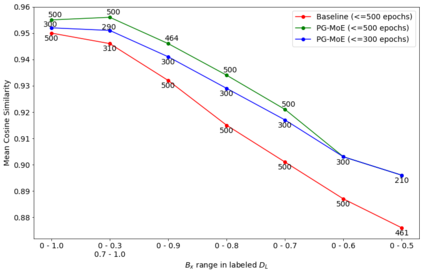
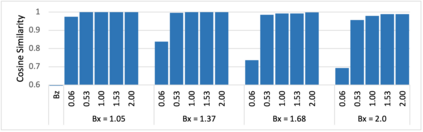
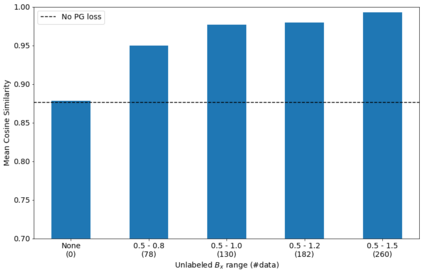
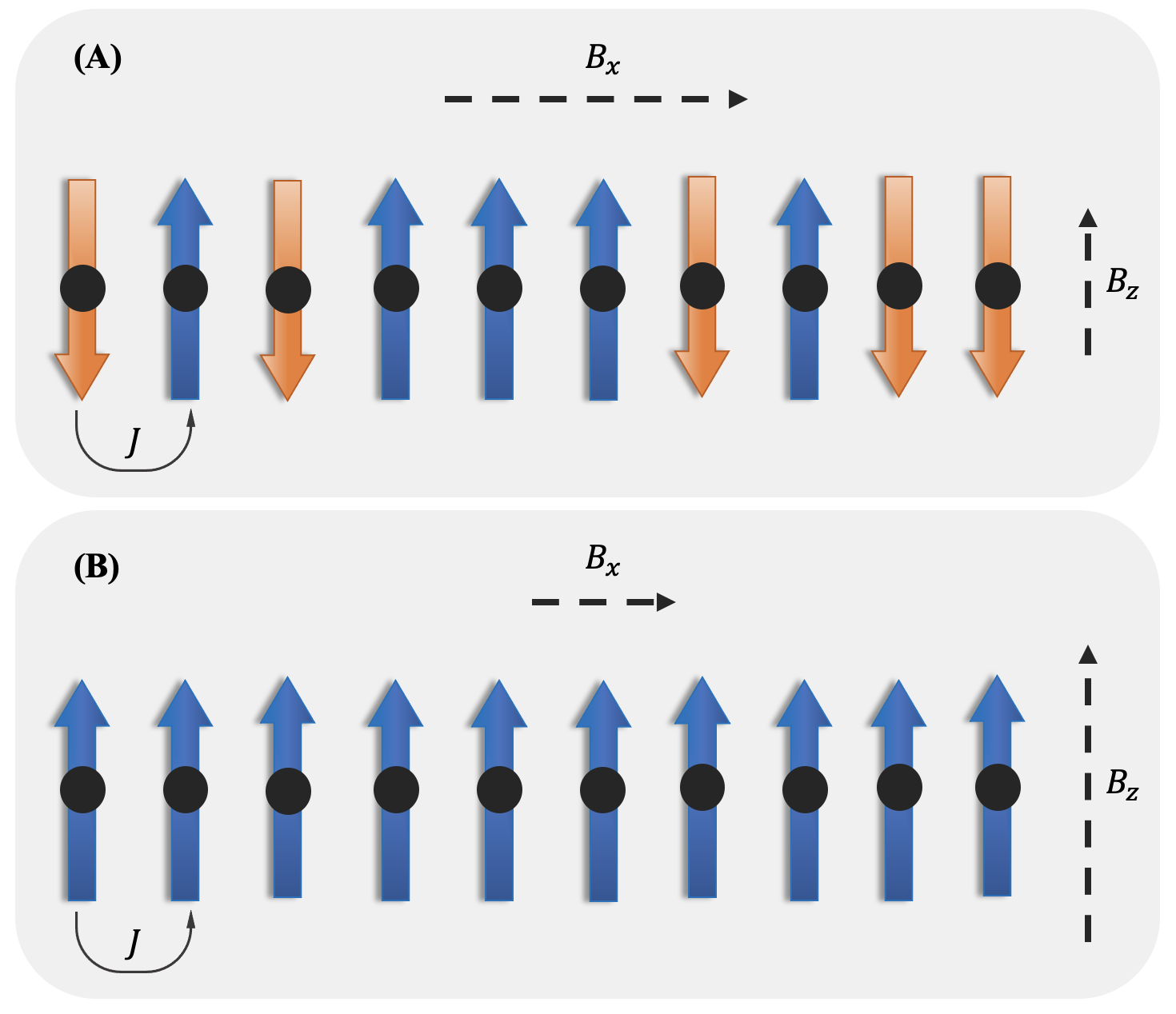
Given their ability to effectively learn non-linear mappings and perform fast inference, deep neural networks (NNs) have been proposed as a viable alternative to traditional simulation-driven approaches for solving high-dimensional eigenvalue equations (HDEs), which are the foundation for many scientific applications. Unfortunately, for the learned models in these scientific applications to achieve generalization, a large, diverse, and preferably annotated dataset is typically needed and is computationally expensive to obtain. Furthermore, the learned models tend to be memory- and compute-intensive primarily due to the size of the output layer. While generalization, especially extrapolation, with scarce data has been attempted by imposing physical constraints in the form of physics loss, the problem of model scalability has remained. In this paper, we alleviate the compute bottleneck in the output layer by using physics knowledge to decompose the complex regression task of predicting the high-dimensional eigenvectors into multiple simpler sub-tasks, each of which are learned by a simple "expert" network. We call the resulting architecture of specialized experts Physics-Guided Mixture-of-Experts (PG-MoE). We demonstrate the efficacy of such physics-guided problem decomposition for the case of the Schr\"{o}dinger's Equation in Quantum Mechanics. Our proposed PG-MoE model predicts the ground-state solution, i.e., the eigenvector that corresponds to the smallest possible eigenvalue. The model is 150x smaller than the network trained to learn the complex task while being competitive in generalization. To improve the generalization of the PG-MoE, we also employ a physics-guided loss function based on variational energy, which by quantum mechanics principles is minimized iff the output is the ground-state solution.
翻译:鉴于它们能够有效地学习非线性绘图并快速进行推断,已提出深神经网络(NNS)作为传统的模拟驱动方法的可行替代方法,以解决作为许多科学应用基础的高维电子价值方程式(HDE),但不幸的是,这些科学应用中学习到的模型通常需要大规模、多样化、最好是附加注释的数据集,而且要获得这些数据集,而且计算成本很高。此外,所学习的模型往往是记忆和计算密集型的,主要由于产出层的大小。虽然试图将数据普遍化,特别是外推,通过物理损失的形式施加物理限制,但模型的伸缩性问题仍然存在。在本文中,我们通过物理知识将高维源数预测的复杂回归任务分解成多个更简单的模型型子任务,其中每一个都是通过简单的“专家”网络的变异性。我们称由此形成的专家更小的物理-基离值的变异性 Elix 电磁性变异性功能也是通过物理学的变异性变异性变异的。