Towards a Numerical Proof of Turbulence Closure

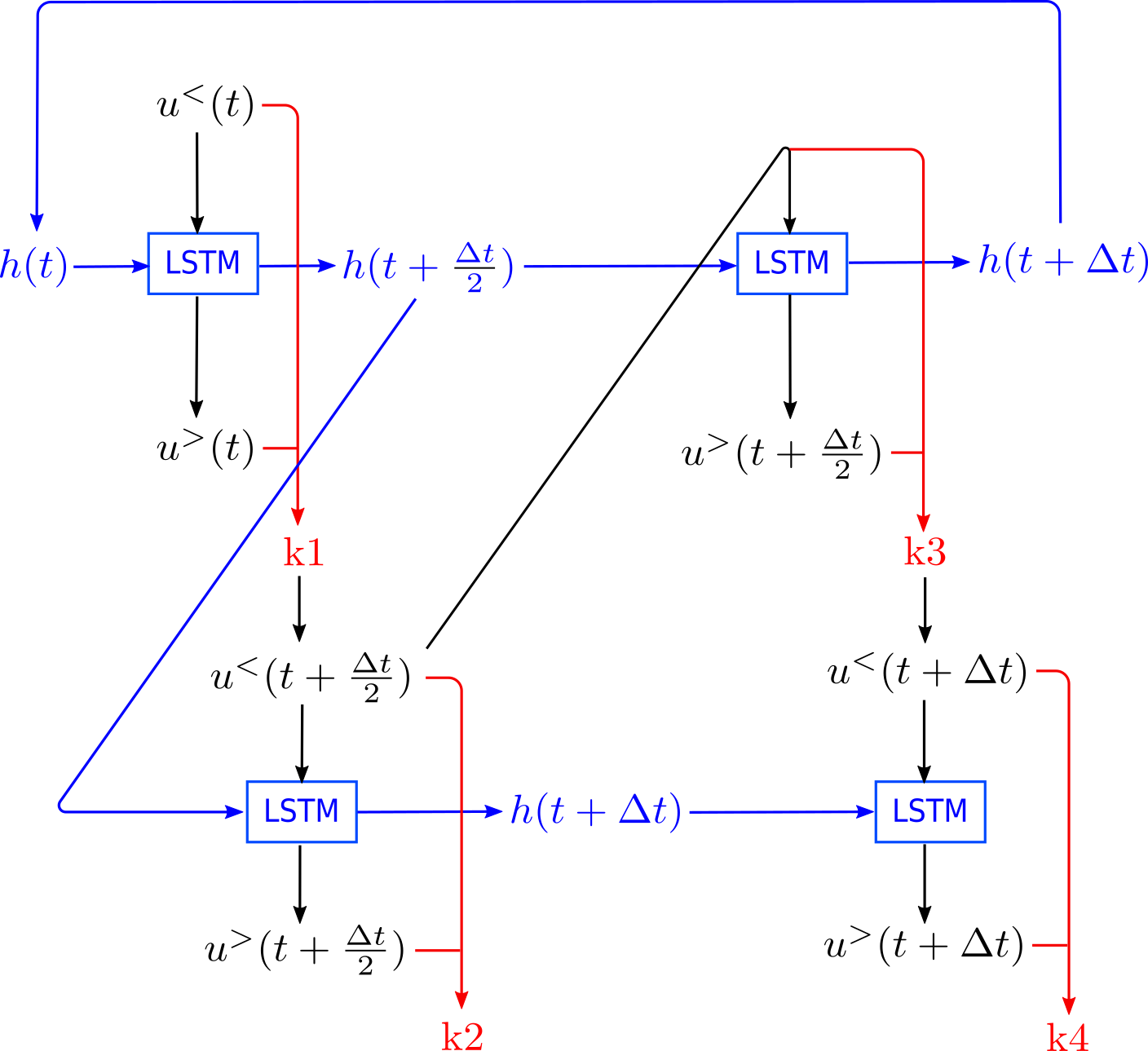
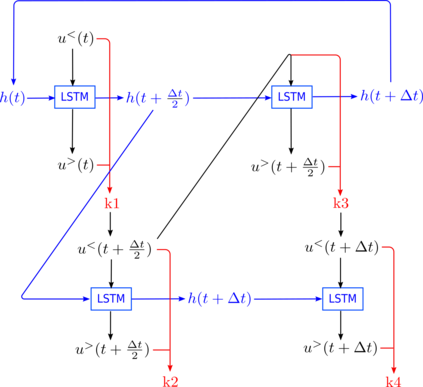
The development of turbulence closure models, parametrizing the influence of small non-resolved scales on the dynamics of large resolved ones, is an outstanding theoretical challenge with vast applicative relevance. We present a closure, based on deep recurrent neural networks, that quantitatively reproduces, within statistical errors, Eulerian and Lagrangian structure functions and the intermittent statistics of the energy cascade, including those of subgrid fluxes. To achieve high-order statistical accuracy, and thus a stringent statistical test, we employ shell models of turbulence. Our results encourage the development of similar approaches for 3D Navier-Stokes turbulence.