Moving sum procedure for change point detection under piecewise linearity

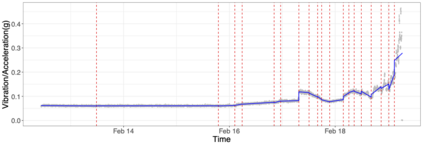
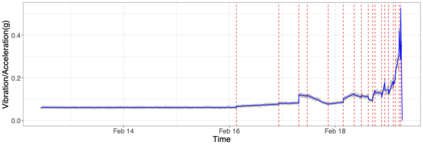
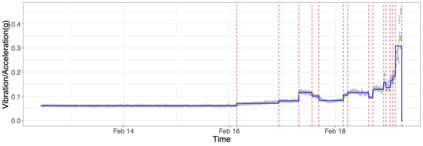
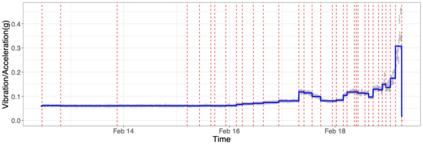
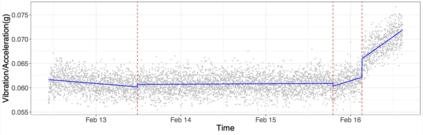
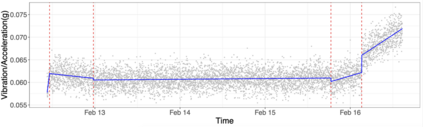
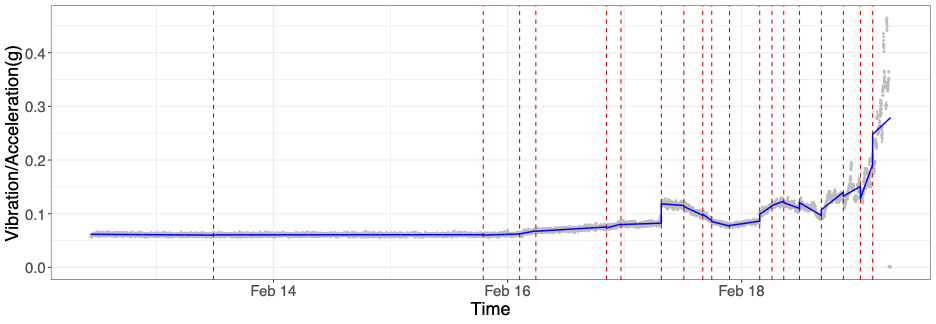
We propose a computationally efficient, moving sum (MOSUM) procedure for segmenting univariate data under piecewise linearity. It detects multiple change points where the underlying signal undergoes discontinuous jumps or slope changes. We show that the proposed method controls the family-wise error rate at a given significance level (asymptotically) and achieves consistency in multiple change point detection, all under weak assumptions permitting heavy-tailedness. We also obtain the rate of localisation when the signal is piecewise linear and continuous, which matches the known minimax optimal rate. Applied to simulated datasets, and a real data example on rolling element-bearing prognostics, the MOSUM procedure performs competitively compared to the existing methods.