A semi-Lagrangian scheme for Hamilton-Jacobi-Bellman equations with oblique boundary conditions

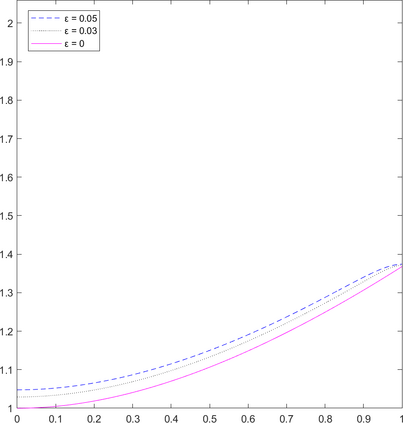
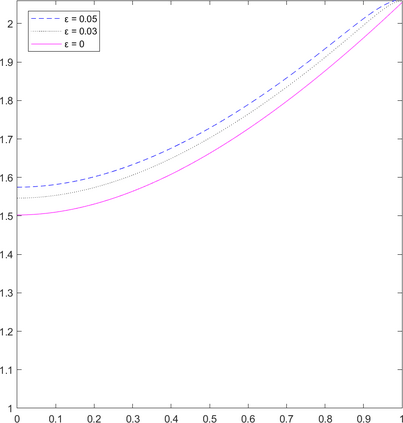
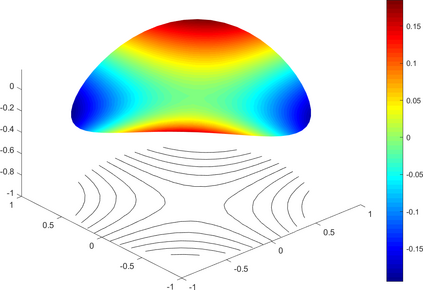
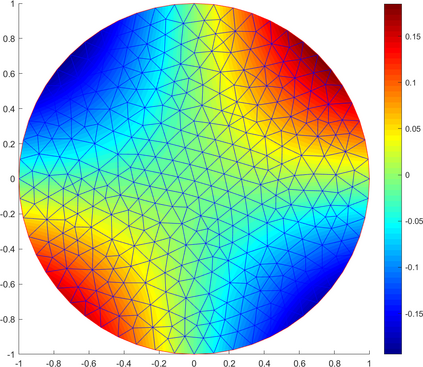
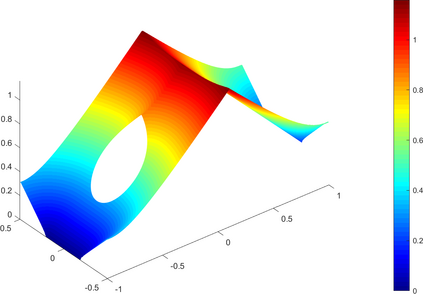
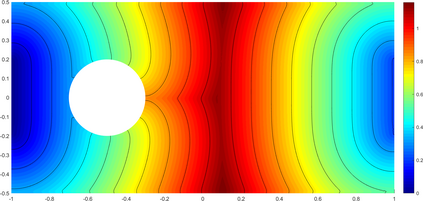
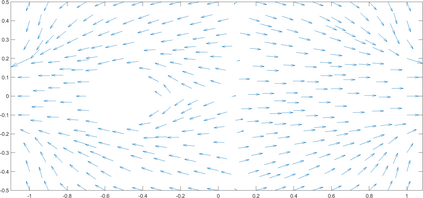
We investigate in this work a fully-discrete semi-Lagrangian approximation of second order possibly degenerate Hamilton-Jacobi-Bellman (HJB) equations on a bounded domain with oblique boundary conditions. These equations appear naturally in the study of optimal control of diffusion processes with oblique reflection at the boundary of the domain. The proposed scheme is shown to satisfy a consistency type property, it is monotone and stable. Our main result is the convergence of the numerical solution towards the unique viscosity solution of the HJB equation. The convergence result holds under the same asymptotic relation between the time and space discretization steps as in the classical setting for semi-Lagrangian schemes. We present some numerical results that confirm the numerical convergence of the scheme.