Adjusting the Benjamini-Hochberg method for controlling the false discovery rate in knockoff assisted variable selection

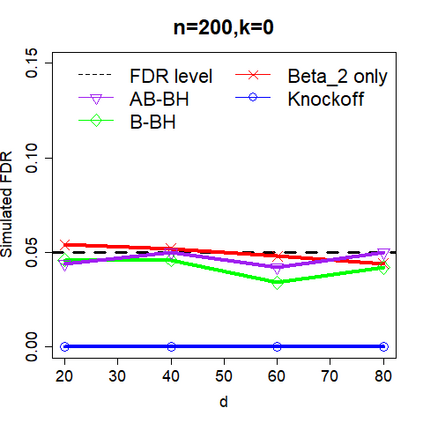
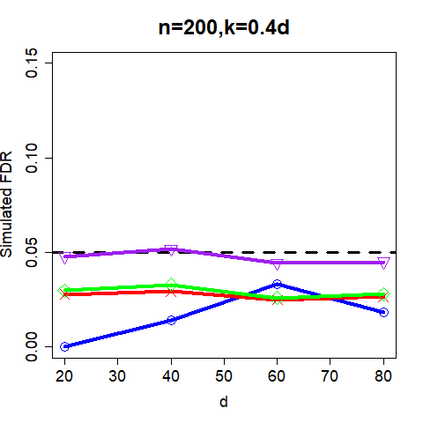
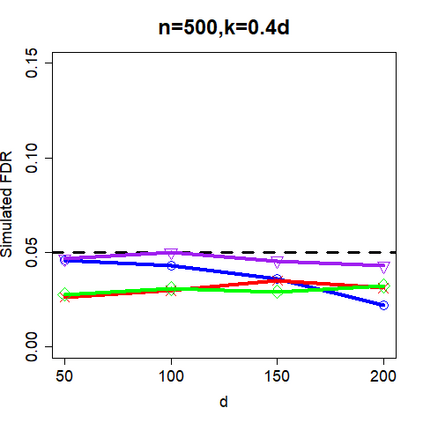
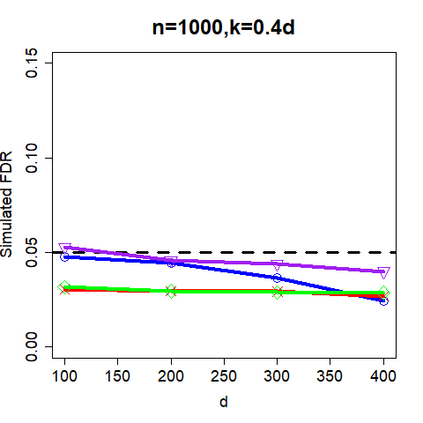
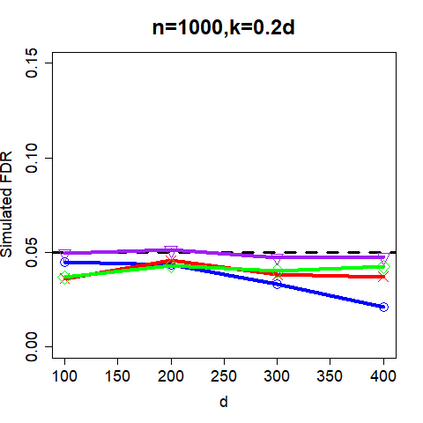
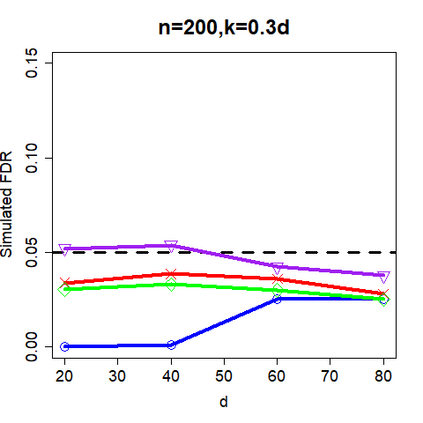
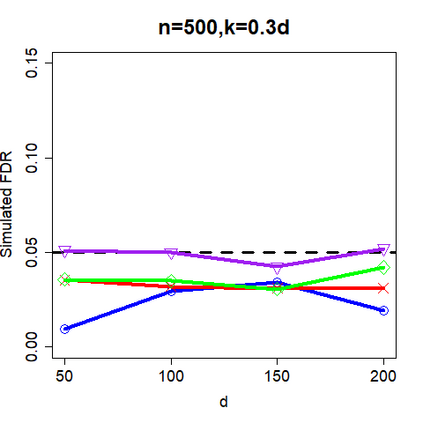
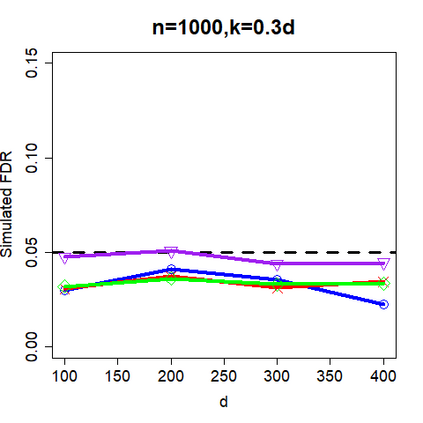
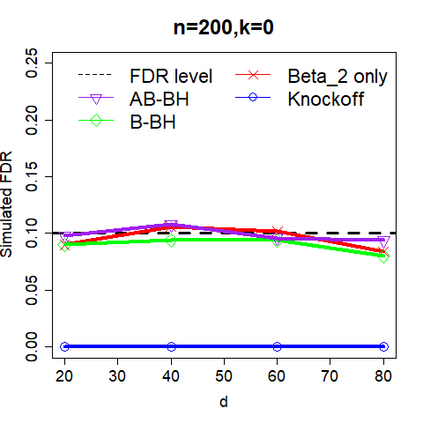
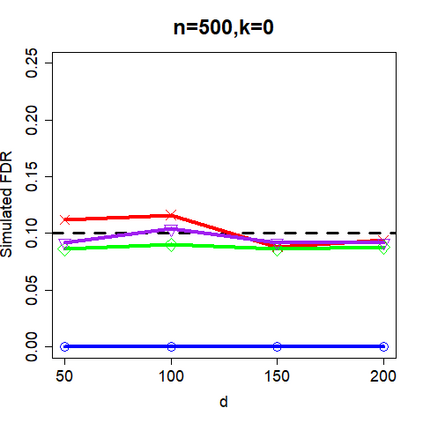
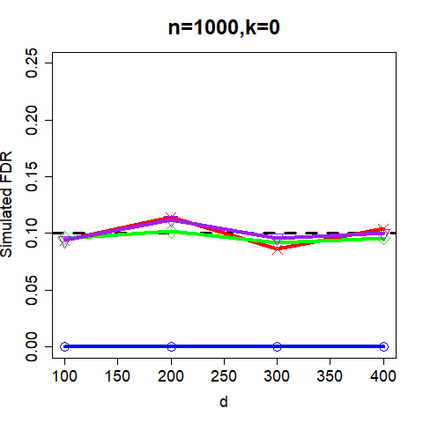
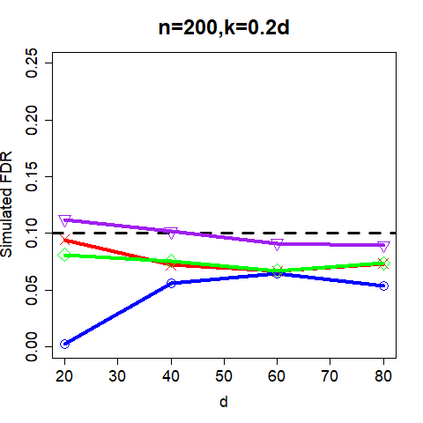
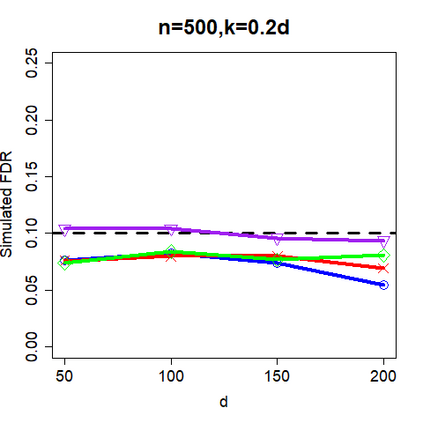
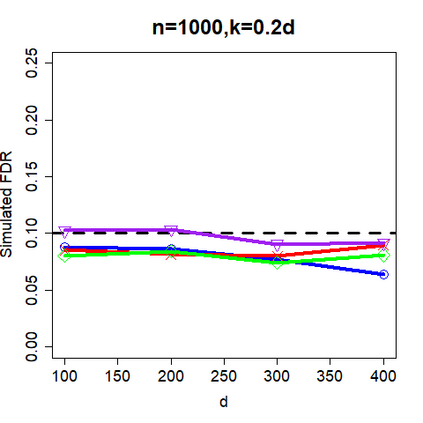
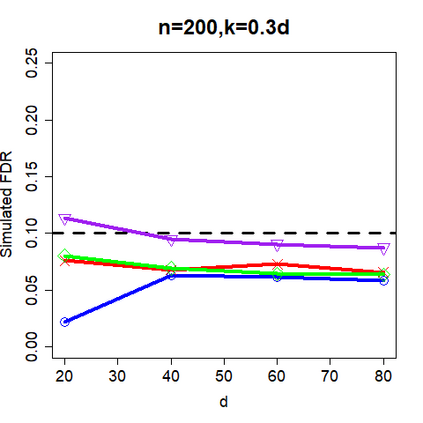
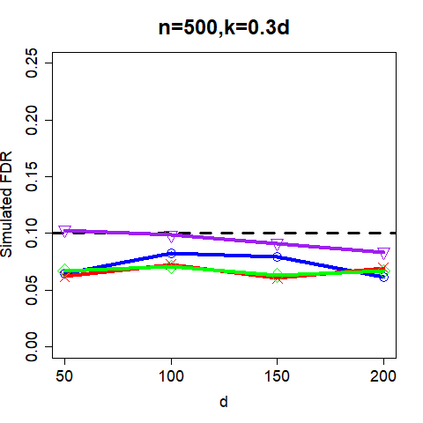
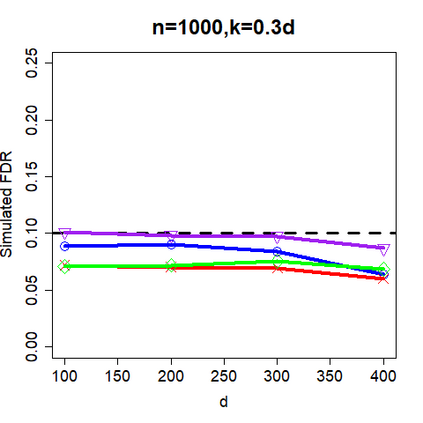
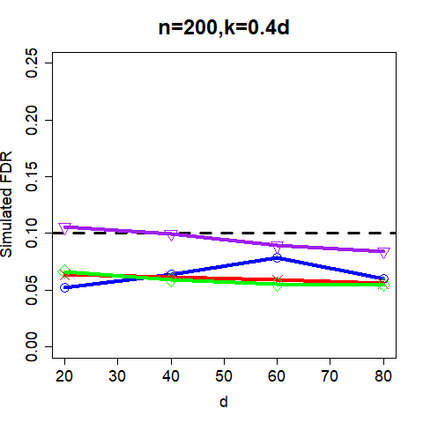
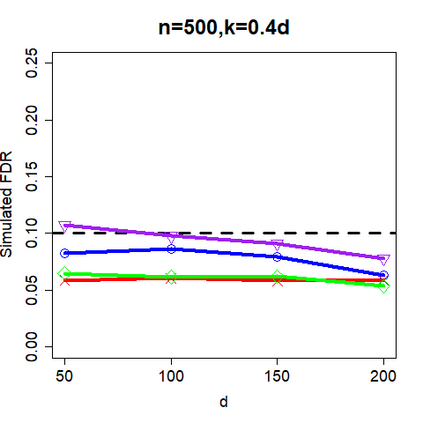
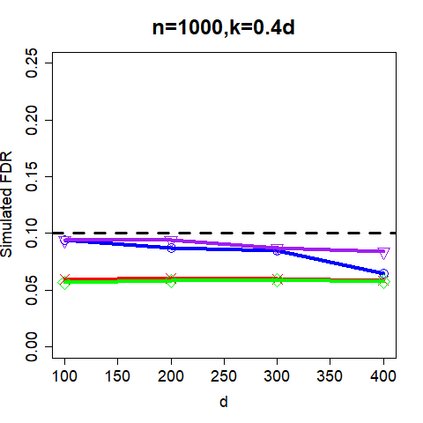
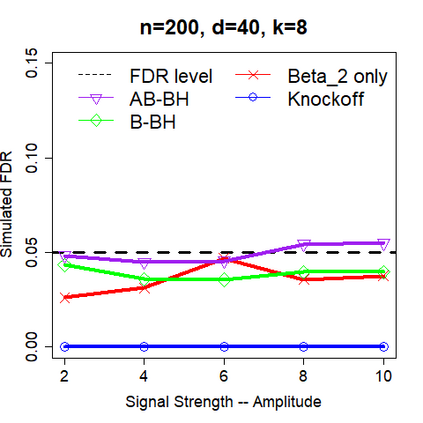
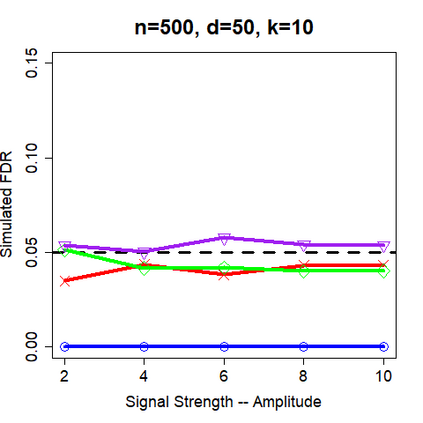
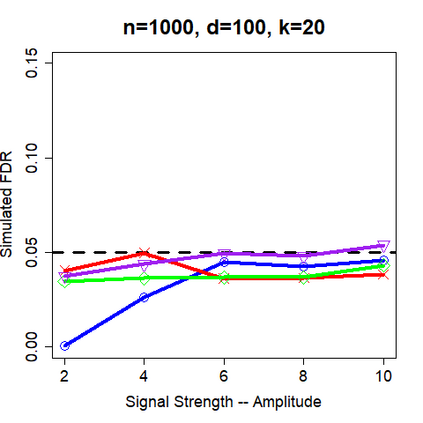
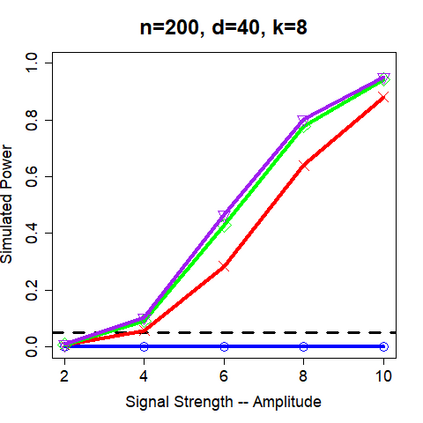
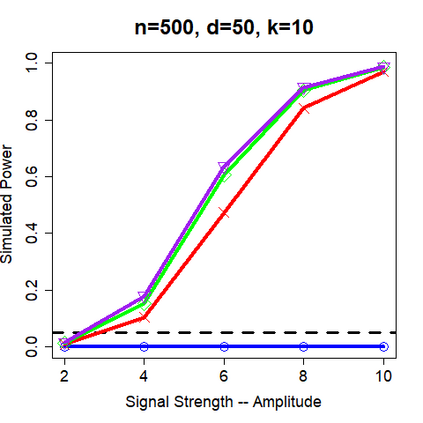
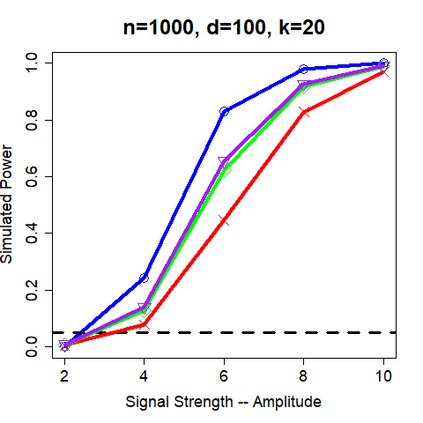
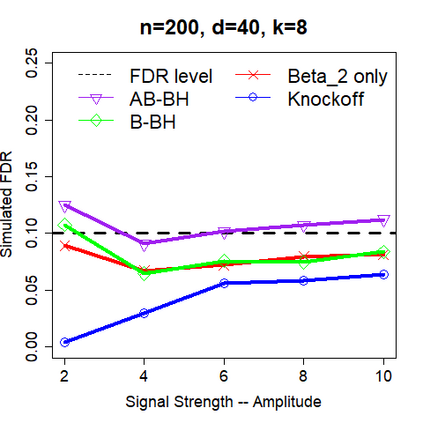
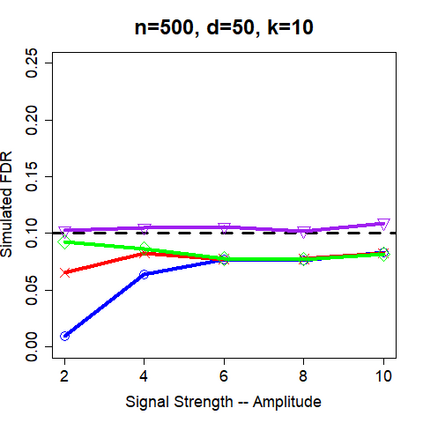
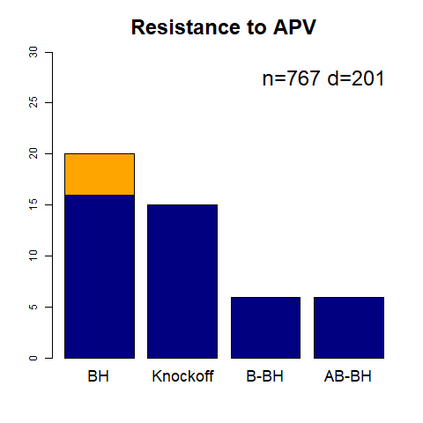
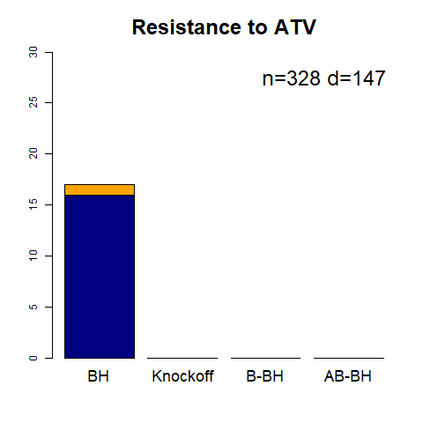
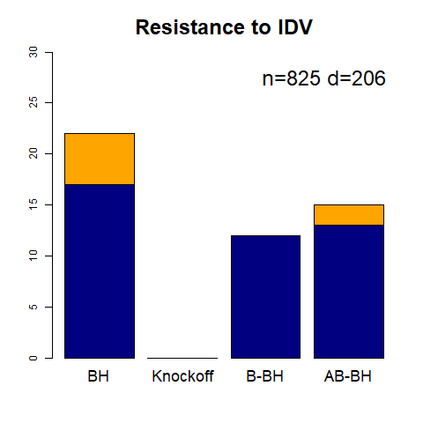
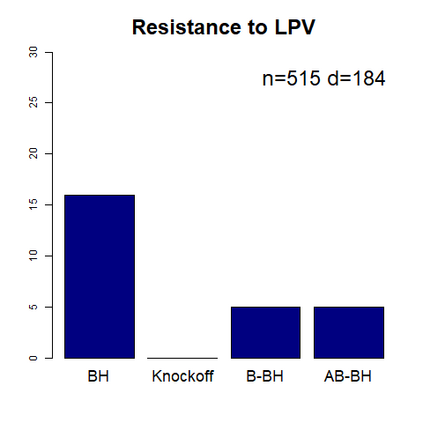
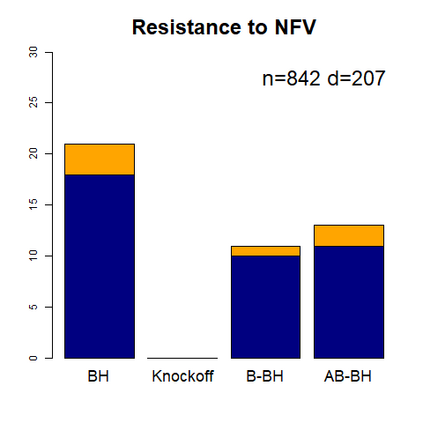
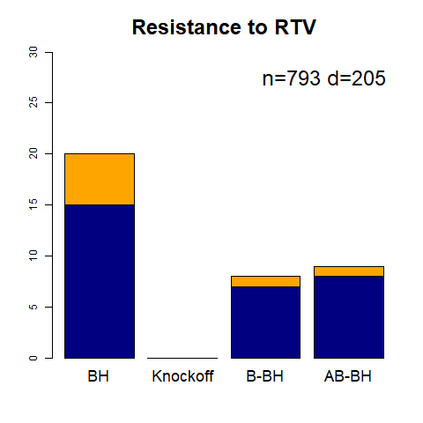
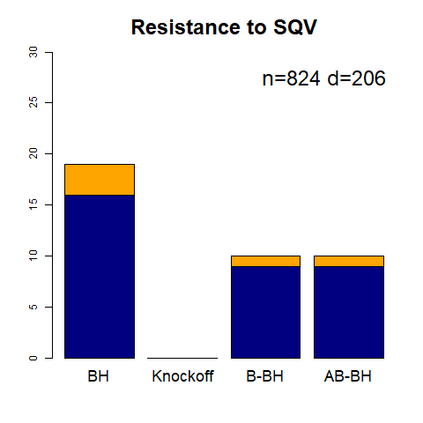
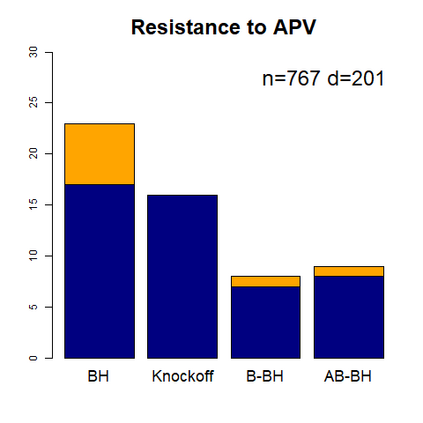
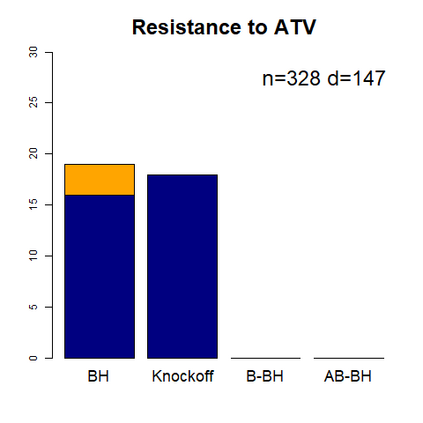
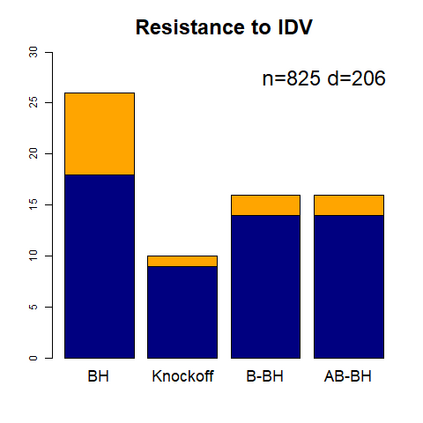
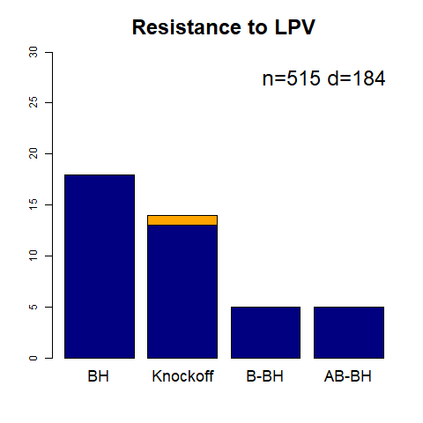
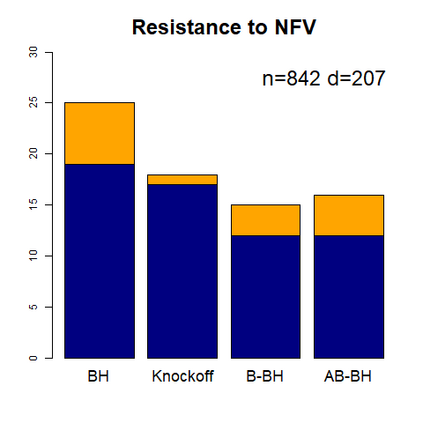
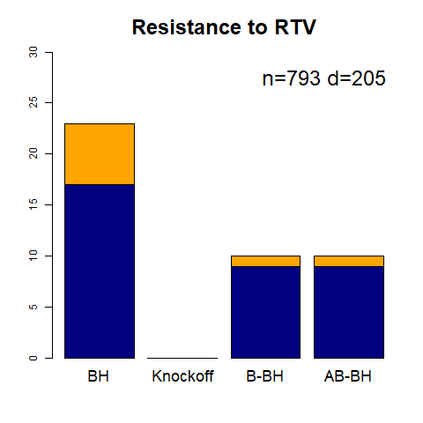
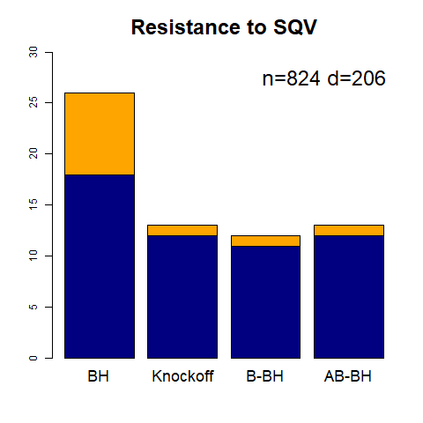
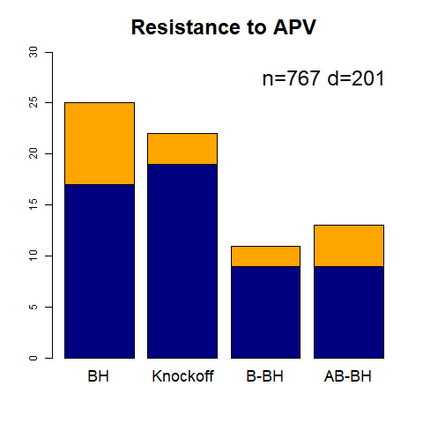
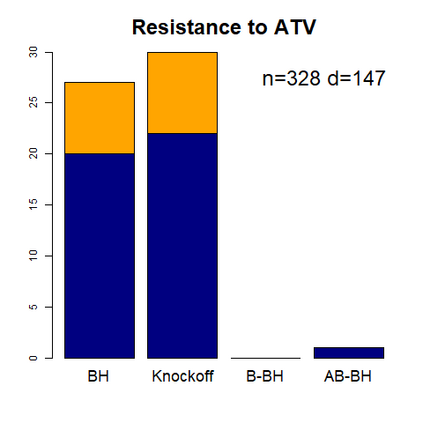
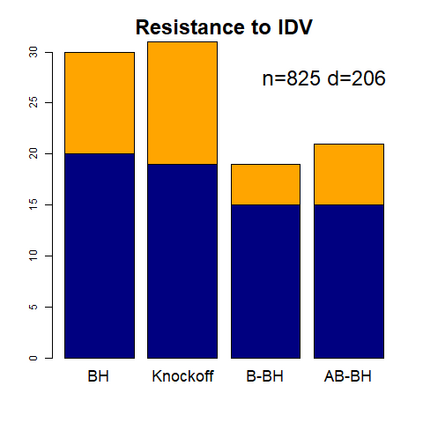
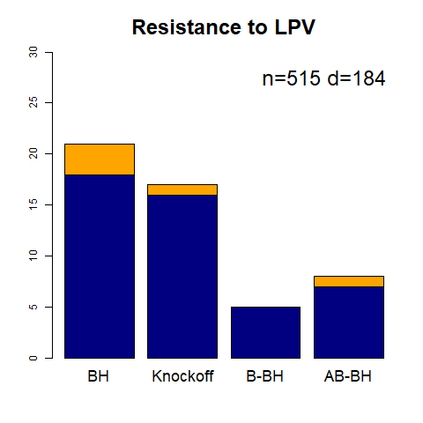
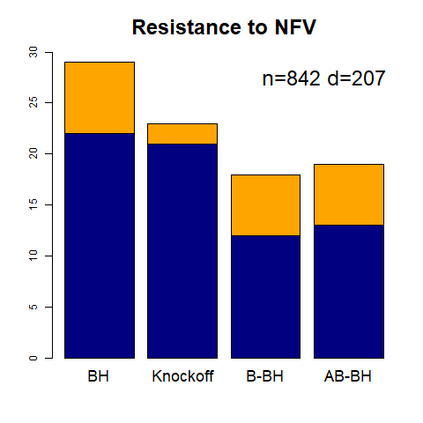
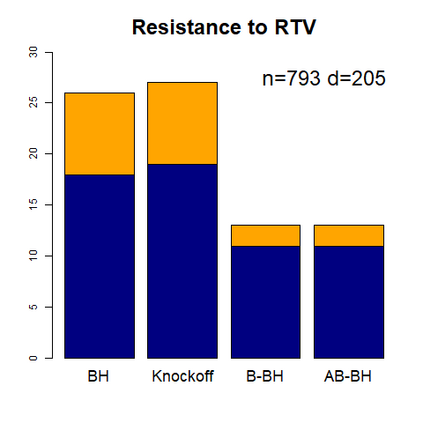
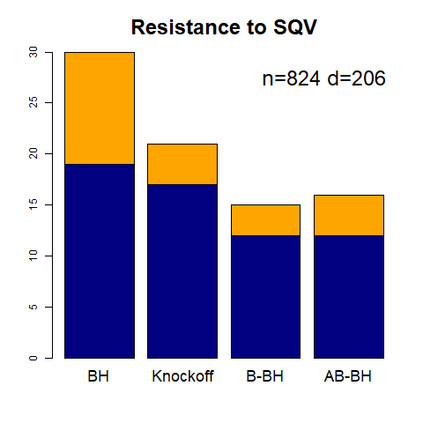
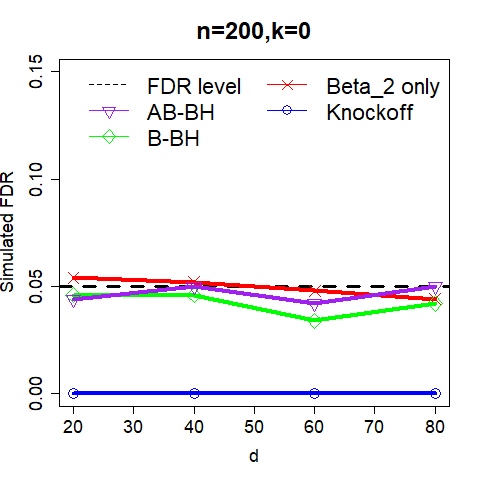
This paper revisits the knockoff-based multiple testing setup considered in Barber & Candes (2015) for variable selection applied to a linear regression model with $n\ge 2d$, where $n$ is the sample size and $d$ is the number of explanatory variables. The BH method based on ordinary least squares estimates of the regressions coefficients is adjusted to this setup, making it a valid $p$-value based FDR controlling method that does not rely on any specific correlation structure of the explanatory variables. Simulations and real data applications demonstrate that our proposed method in its original form and its data-adaptive version incorporating estimated proportion of truly unimportant explanatory variables are powerful competitors of the FDR controlling methods in Barber & Candes (2015).