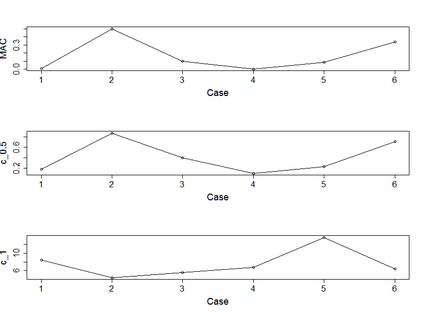
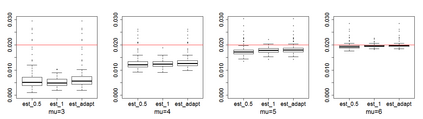
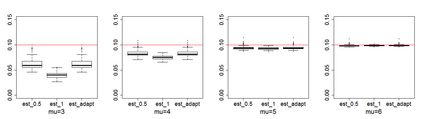
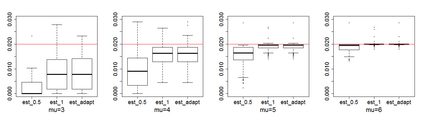
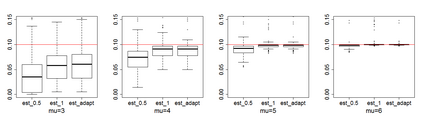
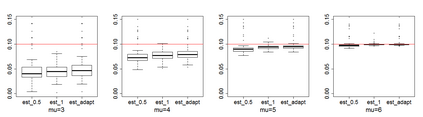
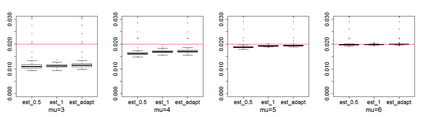
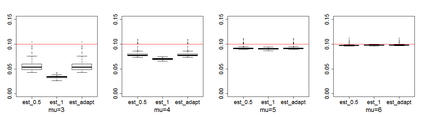
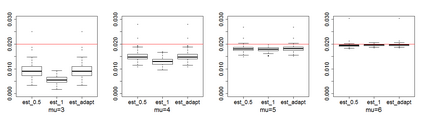
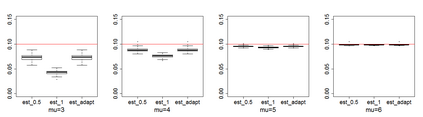
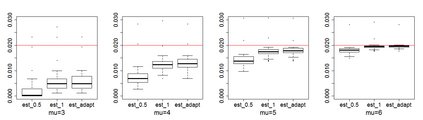
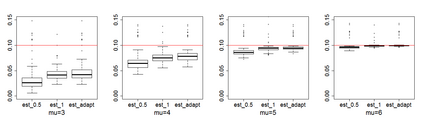
Estimating the proportion of signals hidden in a large amount of noise variables is of interest in many scientific inquires. In this paper, we consider realistic but theoretically challenging settings with arbitrary covariance dependence between variables. We define mean absolute correlation (MAC) to measure the overall dependence level and investigate a family of estimators for their performances in the full range of MAC. We explicit the joint effect of MAC dependence and signal sparsity on the performances of the family of estimators and discover that no single estimator in the family is most powerful under different MAC dependence levels. Informed by the theoretical insight, we propose a new estimator to better adapt to arbitrary covariance dependence. The proposed method compares favorably to several existing methods in extensive finite-sample settings with strong to weak covariance dependence and real dependence structures from genetic association studies.
翻译:估计大量噪音变数中隐藏的信号比例是许多科学调查中感兴趣的。本文认为现实但理论上具有挑战性的环境,各变数之间具有任意的共生依赖性。我们定义了绝对相关性(MAC),以衡量总体依赖性水平,并调查一个估计者家庭在MAC全范围内的性能。我们明确了MAC依赖性和信号宽度对估计者家庭的表现的共同影响,并发现在不同的MAC依赖性水平下,家庭中没有一个单一的估算者最强大。根据理论的洞察,我们提出了一个新的估算者,以便更好地适应任意的共生依赖性。拟议方法优于在广泛的有限分布环境中采用的若干现有方法,这些方法对遗传协会研究的脆弱共生依赖性和实际依赖性结构非常弱。