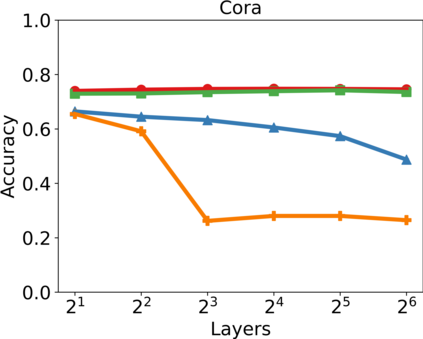
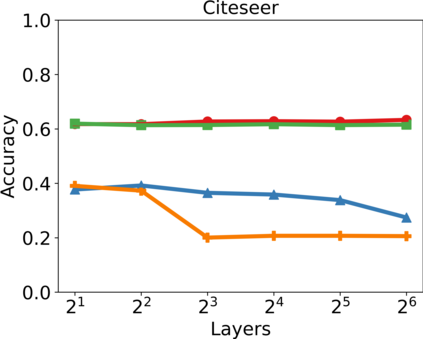
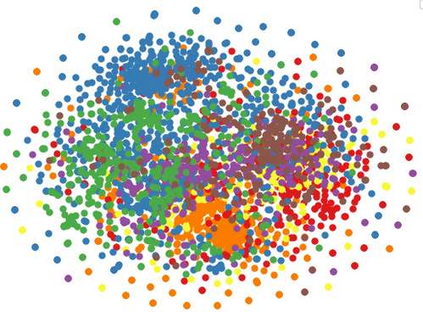
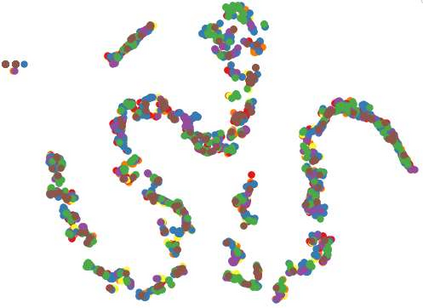
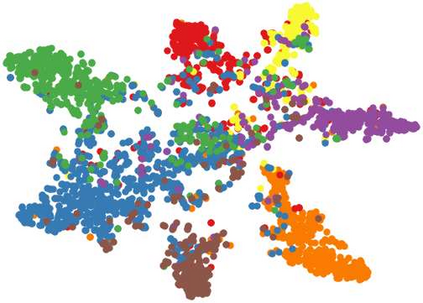
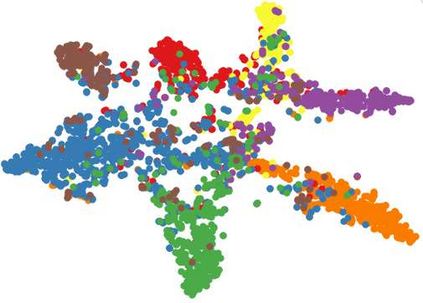
In recent years, hypergraph learning has attracted great attention due to its capacity in representing complex and high-order relationships. However, current neural network approaches designed for hypergraphs are mostly shallow, thus limiting their ability to extract information from high-order neighbors. In this paper, we show both theoretically and empirically, that the performance of hypergraph neural networks does not improve as the number of layers increases, which is known as the over-smoothing problem. To avoid this issue, we develop a new deep hypergraph convolutional network called Deep-HGCN, which can maintain the heterogeneity of node representation in deep layers. Specifically, we prove that a $k$-layer Deep-HGCN simulates a polynomial filter of order $k$ with arbitrary coefficients, which can relieve the problem of over-smoothing. Experimental results on various datasets demonstrate the superior performance of the proposed model compared to the state-of-the-art hypergraph learning approaches.
翻译:近年来,高音学因其代表复杂和高度秩序关系的能力而引起极大关注。然而,目前为高电学设计的神经网络方法大多是浅浅的,从而限制了它们从高电波邻居那里提取信息的能力。在本文中,我们从理论上和从经验上都表明,高电波神经网络的性能并没有随着层数的增加而改善,而这种增加被称为过度移动的问题。为了避免这一问题,我们开发了一个新的深电波深度高电波网络,这个网络可以维持深层节点代表的异质性。具体地说,我们证明,一个价值为千元的深电流网络模拟了一个带有任意系数的单价一K的多元过滤器,可以缓解过度移动的问题。各种数据集的实验结果表明,与最先进的高电压学习方法相比,拟议模型的优异性表现。