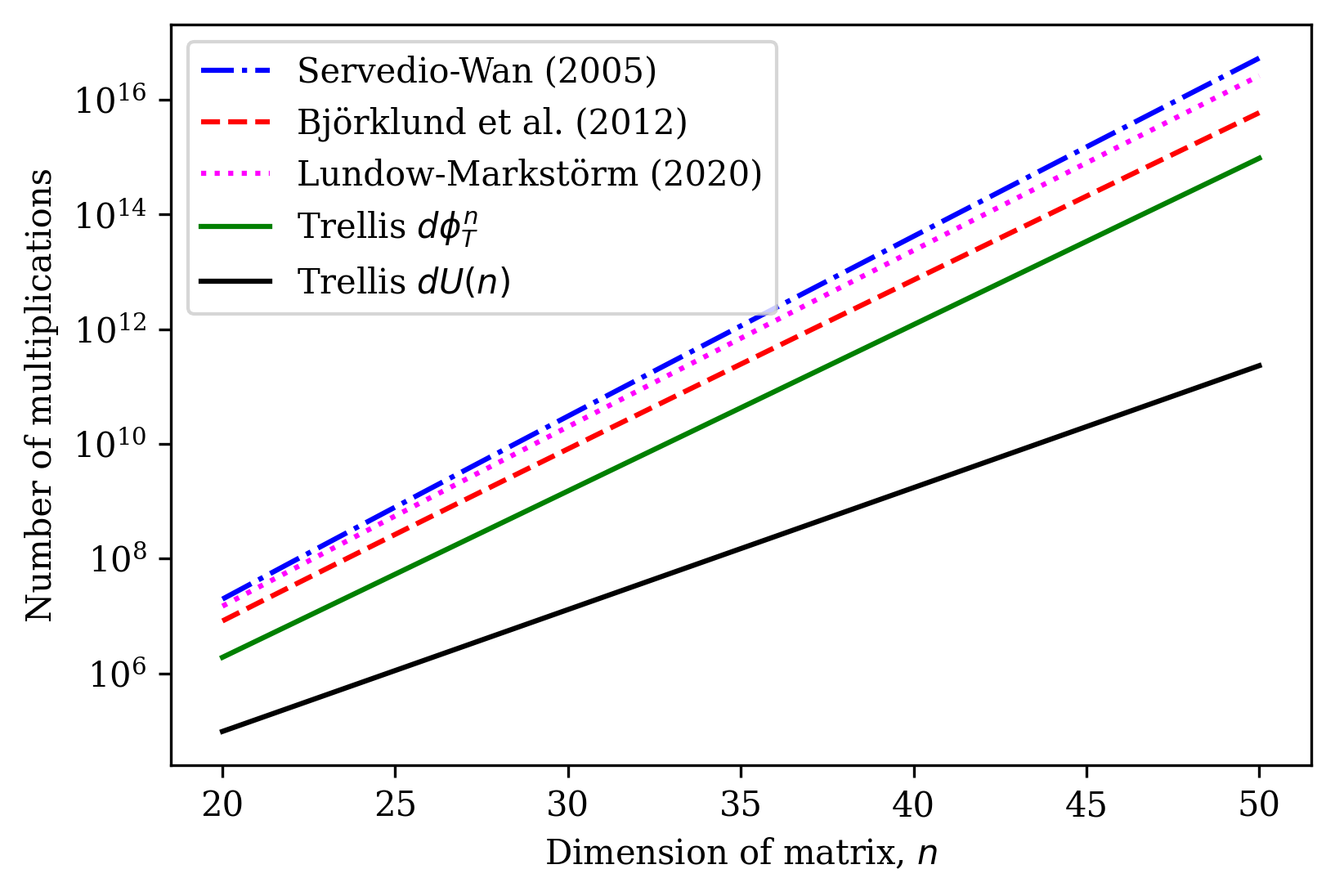
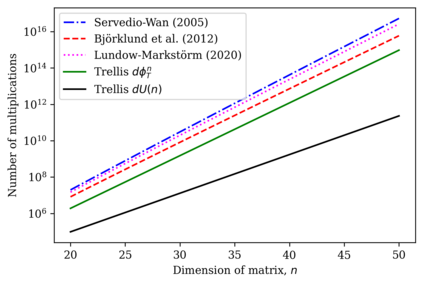
The problem of computing the permanent of a matrix has attracted interest since the work of Ryser(1963) and Valiant(1979). On the other hand, trellises were extensively studied in coding theory since the 1960s. In this work, we establish a connection between the two domains. We introduce the canonical trellis $T_n$ that represents all permutations, and show that the permanent of a $n$ by $n$ matrix $A$ can be computed as a flow on this trellis. Under certain normalization, the trellis-based method invokes slightly less operations than best known exact methods. Moreover, if $A$ has structure, then $T_n$ becomes amenable to vertex merging, thereby significantly reducing its complexity. - Repeated rows: Suppose $A$ has only $t<n$ distinct rows. The best known method to compute $per(A)$, due to Clifford and Clifford (2020), has complexity $O(n^{t+1})$. Merging vertices in $T_n$, we obtain a reduced trellis that has complexity $O(n^t)$. - Order statistics: Using trellises, we compute the joint distribution of $t$ order statistics of $n$ independent, but not identically distributed, random variables in time $O(n^{t+1})$. Previously, polynomial-time methods were known only when the variables are drawn from two non-identical distributions. - Sparse matrices: Suppose each entry in $A$ is nonzero with probability $d/n$ with $d$ is constant. We show that $T_n$ can be pruned to exponentially fewer vertices, resulting in complexity $O(\phi^n)$ with $\phi<2$. - TSP: Intersecting $T_n$ with another trellis that represents walks, we obtain a trellis that represents circular permutations. Using the latter trellis to solve the traveling salesperson problem recovers the well-known Held-Karp algorithm. Notably, in all cases, the reduced trellis are obtained using known techniques in trellis theory. We expect other trellis-theoretic results to apply to other structured matrices.
翻译:自 Ryser (1963年) 和 Valiant (1979年) 的工作以来,计算一个永久矩阵的问题引起了人们的兴趣。 另一方面,自1960年代以来,在编码理论中广泛研究了tellises。 在这项工作中,我们建立了两个域之间的连接。 我们引入了代表所有变式的cancial tellisils $T_n美元。 并显示, 以美元计算一个固定的美元矩阵的永久( 美元) $A美元可以作为这个tellisils 的流流。 在某种常规情况下, 以tellism 为基础的方法比已知的精确方法少一点操作。 此外, 如果 $A 已经设置了 美元, 那么美元 美元 美元 美元, 那么美元 美元 美元 则可以自动计算 。 当我们用trecial_ dicentral discreal discrives 时, 我们用一个已知的treal- discreal discrivers a ral rivers a translations dremod.