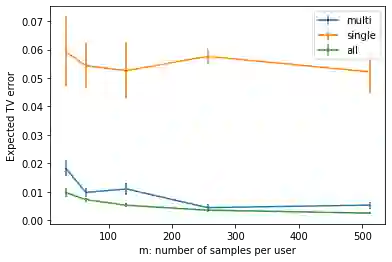
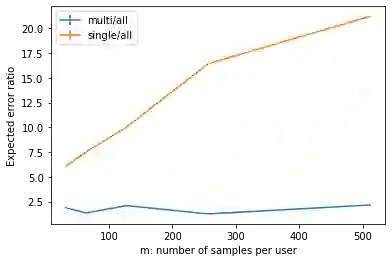
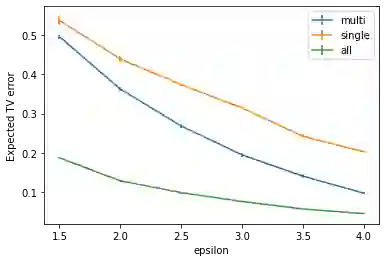
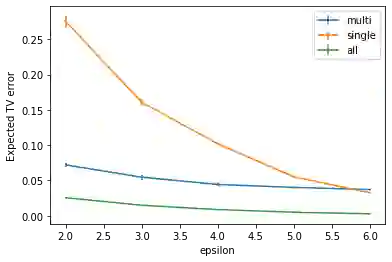
We study discrete distribution estimation under user-level local differential privacy (LDP). In user-level $\varepsilon$-LDP, each user has $m\ge1$ samples and the privacy of all $m$ samples must be preserved simultaneously. We resolve the following dilemma: While on the one hand having more samples per user should provide more information about the underlying distribution, on the other hand, guaranteeing the privacy of all $m$ samples should make the estimation task more difficult. We obtain tight bounds for this problem under almost all parameter regimes. Perhaps surprisingly, we show that in suitable parameter regimes, having $m$ samples per user is equivalent to having $m$ times more users, each with only one sample. Our results demonstrate interesting phase transitions for $m$ and the privacy parameter $\varepsilon$ in the estimation risk. Finally, connecting with recent results on shuffled DP, we show that combined with random shuffling, our algorithm leads to optimal error guarantees (up to logarithmic factors) under the central model of user-level DP in certain parameter regimes. We provide several simulations to verify our theoretical findings.
翻译:我们根据用户一级的当地差异隐私(LDP)研究离散分布估计。在用户级的$varepsilon$-LDP中,每个用户都有1美元样本,必须同时保存所有美元样本的隐私。我们解决了以下两难:一方面,每个用户拥有更多样本,应当提供关于基本分布的更多信息,另一方面,保障所有样本的隐私,应当使估算任务更加困难。在几乎所有参数制度下,我们获得了这一问题的严格界限。也许令人惊讶的是,我们显示在适当的参数制度中,每个用户拥有1美元的样本,相当于每个用户拥有1倍多的1美元样本。我们的结果显示了以1美元和估算风险中的隐私参数为单位的有趣的阶段过渡。最后,我们结合了最近关于摇晃的DP的结果,我们显示了与随机抖动相结合的算法导致在某些参数系统中的用户级DP中心模型下的最佳错误保证(达到对数系数 ) 。我们提供了一些模拟,以核实我们的理论结论。