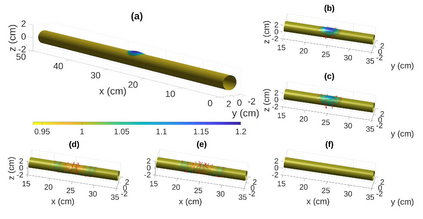
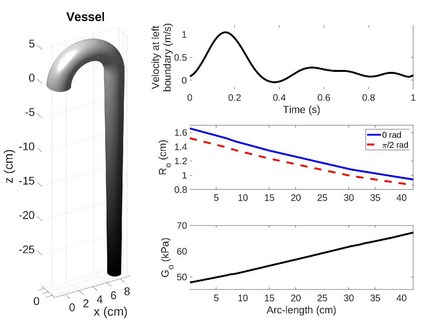
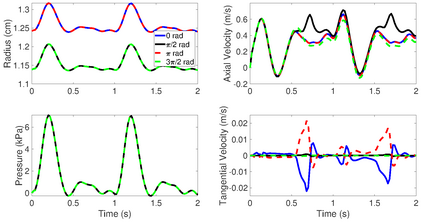
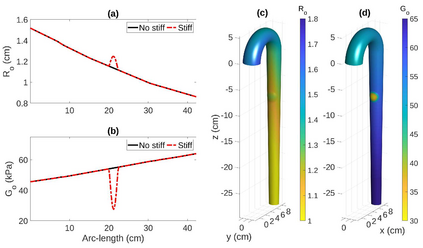
A new two-dimensional model for blood flows in arteries with arbitrary cross sections is derived. The model consists of a system of balance laws for conservation of mass and balance of momentum in the axial and angular directions. The equations are derived by applying asymptotic analysis to the incompressible Navier-Stokes equations in narrow, large vessels and integrating in the radial direction in each cross section. The main properties of the system are discussed and a positivity-preserving well-balanced central-upwind scheme is presented. The merits of the scheme will be tested in a variety of scenarios. In particular, numerical results of simulations using an idealized aorta model are shown. We analyze the time evolution of the blood flow under different initial conditions such as perturbations to steady states consisting of a bulging in the vessel's wall. We consider different situations given by distinct variations in the vessel's elasticity.
翻译:该模型由一套平衡法体系组成,用于保护质量,平衡轴向和角方向的势头。这些方程式是通过对狭窄、大型船只的压抑性纳维埃-斯托克斯方程式进行无症状分析,并在每一横截面的射线方向进行整合而得出的。对该系统的主要特性进行了讨论,并提出了一种相对性 -- -- 保留良好平衡的中上风方案。该方法的优点将在各种情景中进行测试。特别是,展示了使用理想化动脉模型进行模拟的数值结果。我们分析了血液流动在不同初始条件下的时间演变,例如,在轮廓的扰动到稳定状态时,形成船只壁上的挤动。我们考虑了不同情况,因为船只弹性的变化不同。