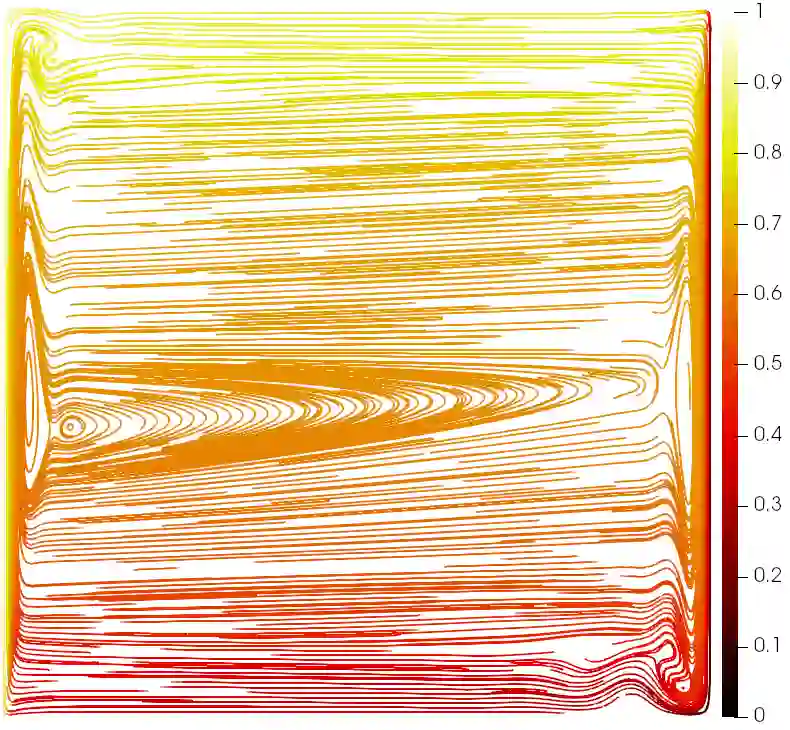
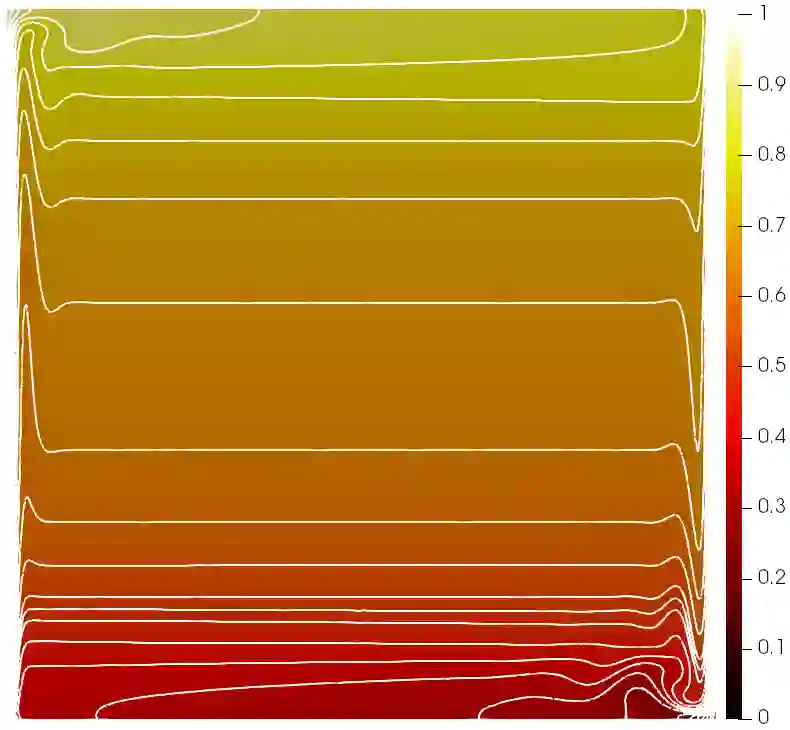
We devise 3-field and 4-field finite element approximations of a system describing the steady state of an incompressible heat-conducting fluid with implicit non-Newtonian rheology. We prove that the sequence of numerical approximations converges to a weak solution of the problem. We develop a block preconditioner based on augmented Lagrangian stabilisation for a discretisation based on the Scott-Vogelius finite element pair for the velocity and pressure. The preconditioner involves a specialised multigrid algorithm that makes use of a space-decomposition that captures the kernel of the divergence and non-standard intergrid transfer operators. The preconditioner exhibits robust convergence behaviour when applied to the Navier-Stokes and power-law systems, including temperature-dependent viscosity, heat conductivity and viscous dissipation.
翻译:我们设计了一个系统,用隐含的非牛顿红心学来描述一种不压缩热导流的稳态状态。我们证明数字近似的顺序与解决问题的薄弱办法相汇合。我们开发了一个基于基于Scott-Vogelius定质元素对速度和压力的分解增强拉格朗加固化的区块先决条件。先决条件包含一个专门化的多格计算法,该算法利用空间分解法来捕捉差异和非标准内格传输操作器的内核。前提条件在应用纳维尔-斯托克和动力法系统时表现出强大的趋同行为,包括依赖温度的粘度、热导力和粘性消化。