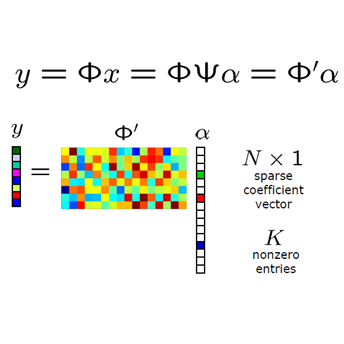
This paper studies the quantization of heavy-tailed data in some fundamental statistical estimation problems, where the underlying distributions have bounded moments of some order. We propose to truncate and properly dither the data prior to a uniform quantization. Our major standpoint is that (near) minimax rates of estimation error are achievable merely from the quantized data produced by the proposed scheme. In particular, concrete results are worked out for covariance estimation, compressed sensing, and matrix completion, all agreeing that the quantization only slightly worsens the multiplicative factor. Besides, we study compressed sensing where both covariate (i.e., sensing vector) and response are quantized. Under covariate quantization, although our recovery program is non-convex because the covariance matrix estimator lacks positive semi-definiteness, all local minimizers are proved to enjoy near optimal error bound. Moreover, by the concentration inequality of product process and covering argument, we establish near minimax uniform recovery guarantee for quantized compressed sensing with heavy-tailed noise.
翻译:暂无翻译