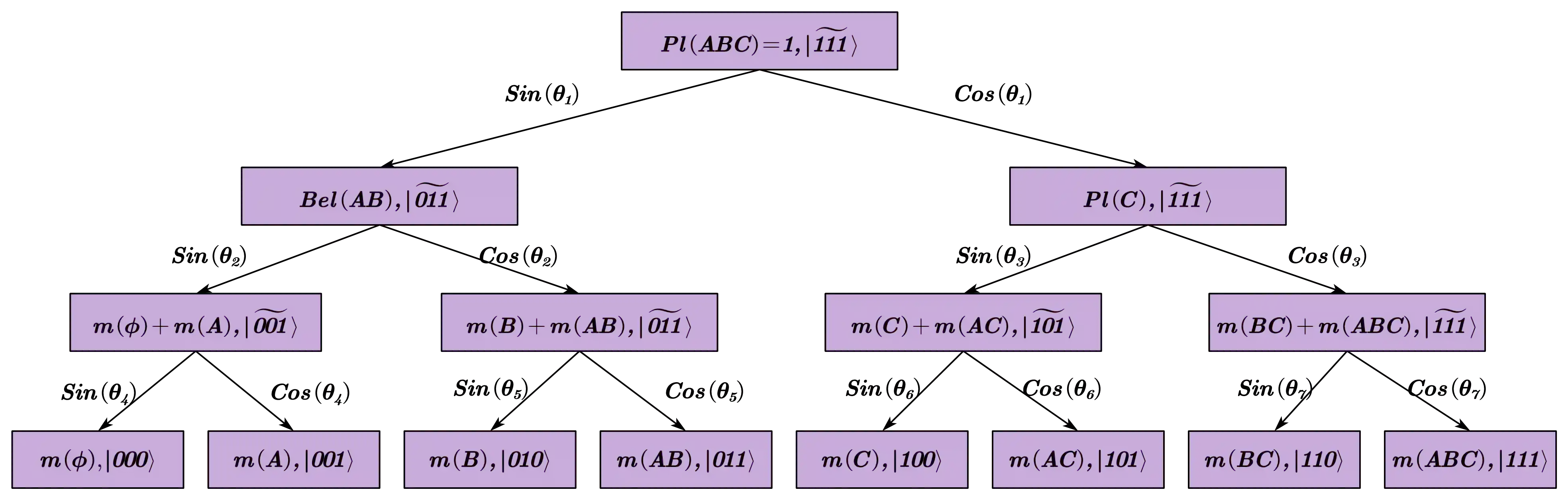
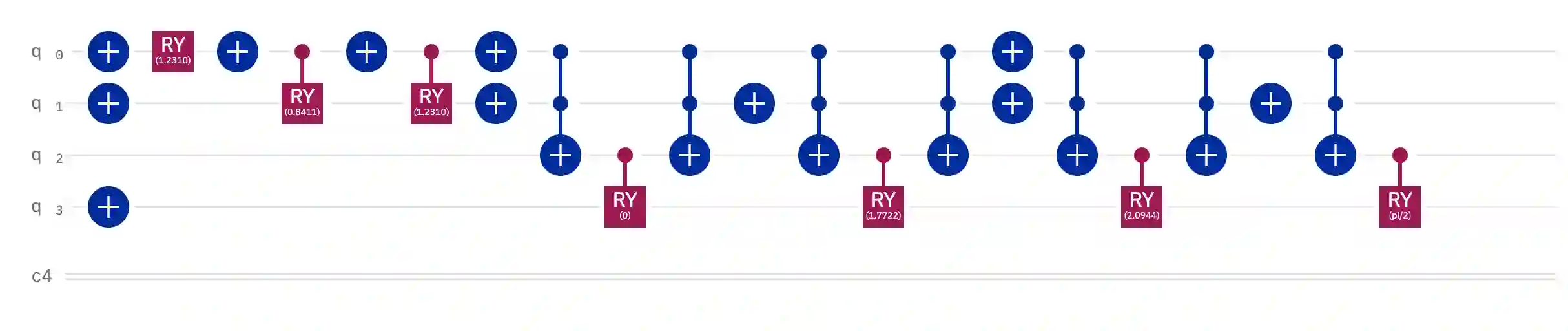
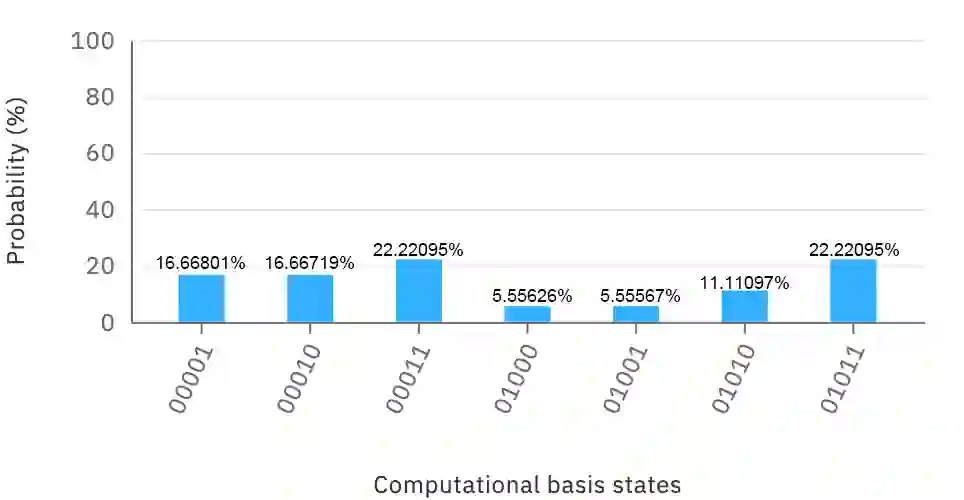
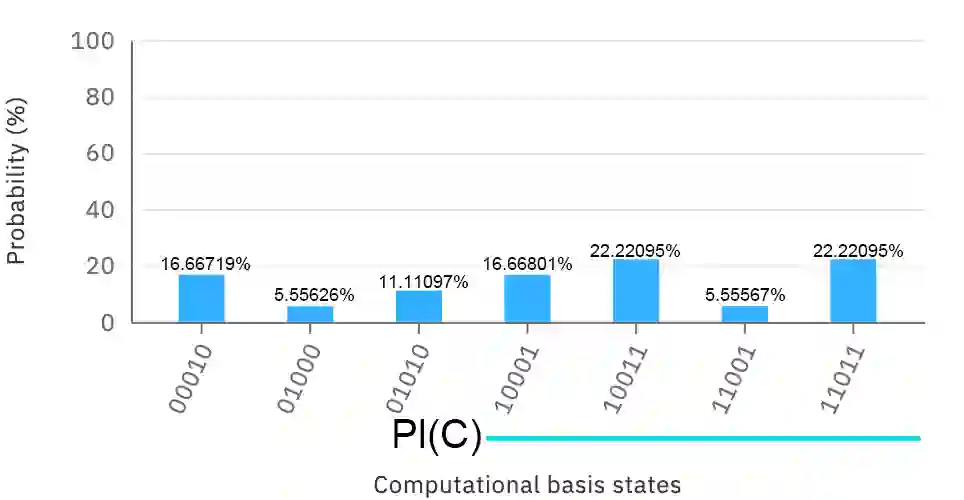
The belief function in Dempster Shafer evidence theory can express more information than the traditional Bayesian distribution. It is widely used in approximate reasoning, decision-making and information fusion. However, its power exponential explosion characteristics leads to the extremely high computational complexity when handling large amounts of elements in classic computers. In order to solve the problem, we encode the basic belief assignment (BBA) into quantum states, which makes each qubit correspond to control an element. Besides the high efficiency, this quantum expression is very conducive to measure the similarity between two BBAs, and the measuring quantum algorithm we come up with has exponential acceleration theoretically compared to the corresponding classical algorithm. In addition, we simulate our quantum version of BBA on Qiskit platform, which ensures the rationality of our algorithm experimentally. We believe our results will shed some light on utilizing the characteristic of quantum computation to handle belief function more conveniently.
翻译:Dempster Shafer 证据理论中的信仰功能可以比传统的巴伊西亚分布法表达更多的信息。 它被广泛用于近似推理、决策和信息融合。 但是,它的电动指数爆炸特性导致在处理经典计算机大量元素时极高的计算复杂性。 为了解决问题,我们把基本信仰分配(BBA)编码成量子状态,使每个Qubit都与控制元素相对应。 除了高效率外,这个量子表达方式非常有利于测量两个BBA和我们制作的量子算法之间的相似性,而我们制作的量子算法在理论上与相应的古典算法相比具有指数加速性加速性。 此外,我们还在基斯基特平台上模拟我们的BBA量子版本,这能确保我们算法的合理性。 我们相信,我们的结果将会为利用量子计算特征来更方便地处理信仰功能提供一些线索。