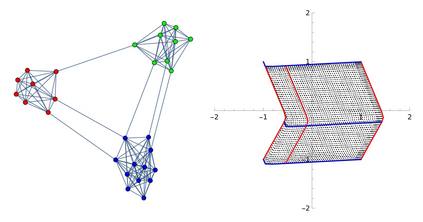
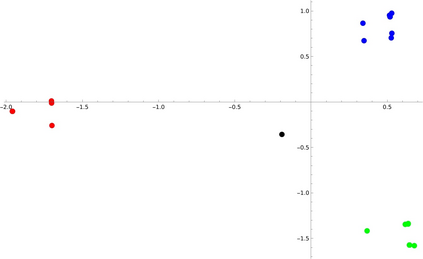
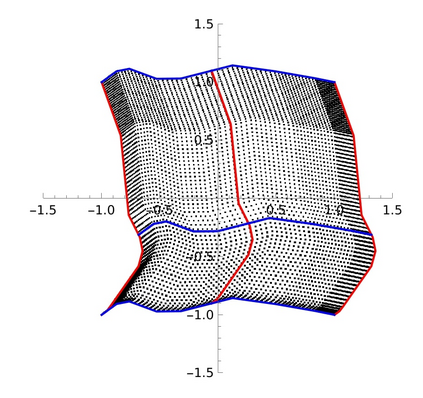
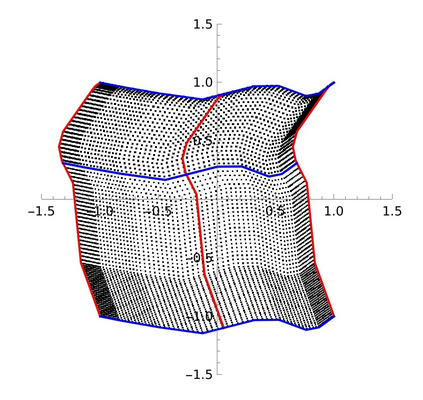
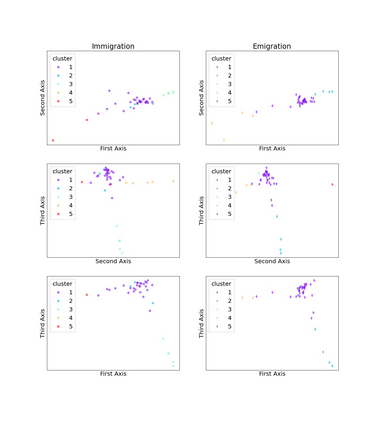
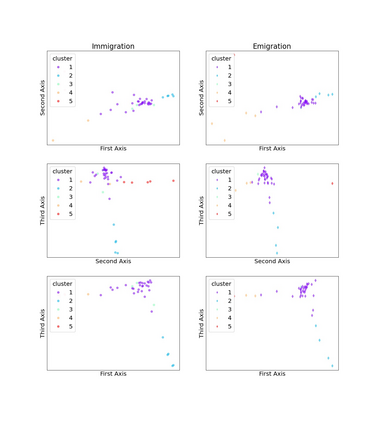
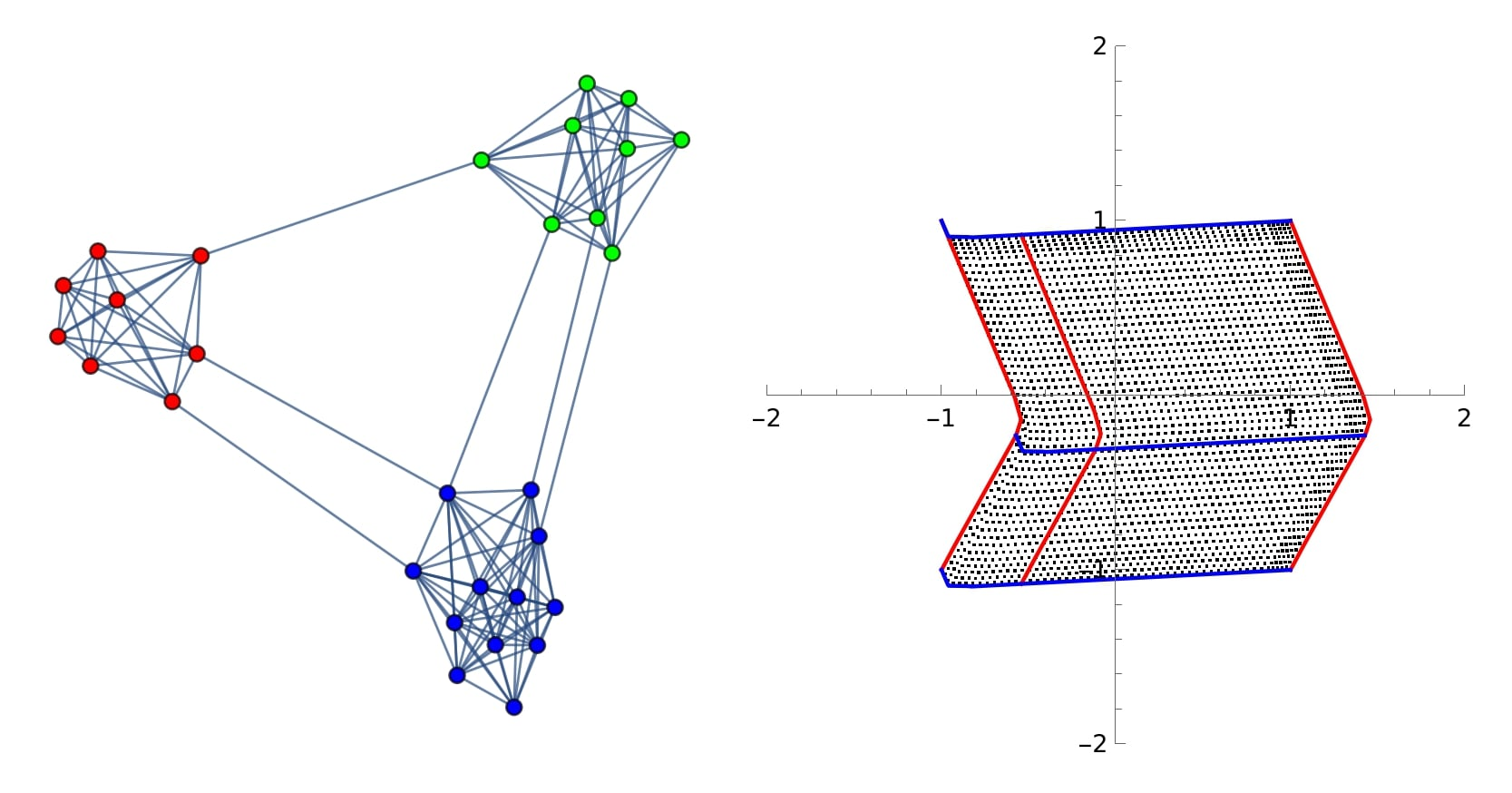
Spectral clustering is discussed from many perspectives, by extending it to rectangular arrays and discrepancy minimization too. Near optimal clusters are obtained with singular value decomposition and with the weighted $k$-means algorithm. In case of rectangular arrays, this means enhancing the method of correspondence analysis with clustering, and in case of edge-weighted graphs, a normalized Laplacian based clustering. In the latter case it is proved that a spectral gap between the $(k-1)$th and $k$th smallest positive eigenvalues of the normalized Laplacian matrix gives rise to a sudden decrease of the inner cluster variances when the number of clusters of the vertex representatives is $2^{k-1}$, but only the first $k-1$ eigenvectors, constituting the so-called Fiedler-carpet, are used in the representation. Application to directed migration graphs is also discussed.
翻译:从许多角度讨论频谱集群,将之扩大到矩形阵列和差异最小化。接近最佳的集群是以单值分解和加权美元平均算法获得的。对于矩形阵列,这意味着加强与集群的对应分析方法,对于边加权图,则意味着一个基于边加权图的标准化拉普拉西亚组合。在后一种情况下,事实证明,在(k-1)美元和(k-1)美元等标准拉普拉西安矩阵最小正值之间的光谱差距导致内部集群差异的突然缩小,因为顶层代表群的数量是2 ⁇ k-1美元,但代表中只使用了构成所谓的Fiedler-carpet的第一批$-1美元电子元。还讨论了定向迁移图的应用。