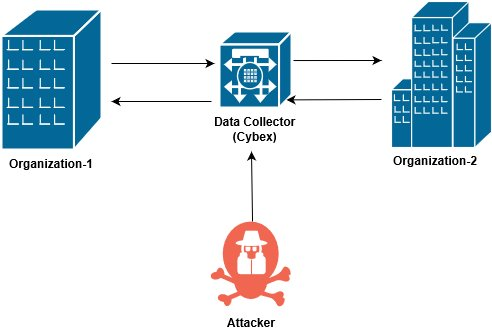
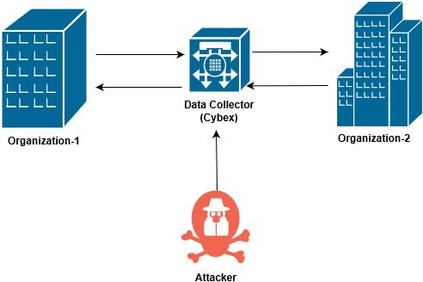
Data sharing between different organizations is an essential process in today's connected world. However, recently there were many concerns about data sharing as sharing sensitive information can jeopardize users' privacy. To preserve the privacy, organizations use anonymization techniques to conceal users' sensitive data. However, these techniques are vulnerable to de-anonymization attacks which aim to identify individual records within a dataset. In this paper, a two-tier mathematical framework is proposed for analyzing and mitigating the de-anonymization attacks, by studying the interactions between sharing organizations, data collector, and a prospective attacker. In the first level, a game-theoretic model is proposed to enable sharing organizations to optimally select their anonymization levels for k-anonymization under two potential attacks: background-knowledge attack and homogeneity attack. In the second level, a contract-theoretic model is proposed to enable the data collector to optimally reward the organizations for their data. The formulated problems are studied under single-time sharing and repeated sharing scenarios. Different Nash equilibria for the proposed game and the optimal solution of the contract-based problem are analytically derived for both scenarios. Simulation results show that the organizations can optimally select their anonymization levels, while the data collector can benefit from incentivizing the organizations to share their data.
翻译:不同组织之间分享数据是当今相互联系的世界中一个必不可少的过程。然而,最近人们对于数据分享有许多关切,因为共享敏感信息会危及用户隐私。为了保护隐私,各组织使用匿名技术来隐藏用户敏感数据。然而,这些技术很容易受到匿名攻击,目的是在数据集中识别个人记录。在本文件中,提议了一个两级数学框架,通过研究共享组织、数据收集员和潜在攻击者之间的互动,来分析和减轻匿名攻击。在第一级,提议了一个游戏理论模型,使共享组织能够在两种潜在攻击(即背景知识攻击和同源攻击)下最佳选择其匿名水平,用于K-匿名化。在第二一级,提议了一个合同理论模型,使数据收集员能够最佳地奖励各组织的数据。在一次性共享和重复共享假设中研究所拟订的问题。提议的游戏和合同问题的最佳解决方案的不同Nash平衡模型,在最佳的假设下,可以从最佳的数据收集者组织的角度进行分析性分析,同时从最佳的数据收集者组织的角度来显示最佳的数据分享水平。