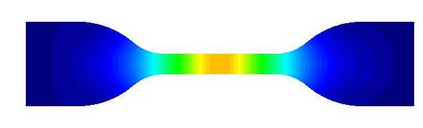
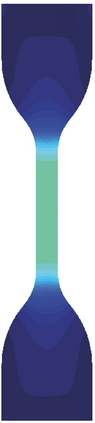This paper proposes a thermodynamically consistent phase-field damage model for viscoelastic materials. Suitable free-energy and pseudo-potentials of dissipation are developed to build a model leading to a stress-strain relation, under the assumption of finite {strain}, in terms of fractional derivatives. A novel degradation function, which properly couples stress response and damage evolution for viscoelastic materials, is proposed. We obtain a set of differential equations that accounts for the evolution of motion, damage, and temperature. In the present work, for simplicity, this model is numerically solved for isothermal cases by using a semi-implicit/explicit scheme. Several numerical tests, including fitting with experimental data, show that the developed model accounts appropriately for damage in viscoelastic materials for small and finite strains. Non-isothermal numerical simulations will be considered in future works.
翻译:本文为粘合弹性材料提出了一个热动力一致的相位损害模型。开发了一个合适的自由能源和假的散射潜力模型,以建立一个模型,在有限的{strain}假设下,在分衍生物方面形成压力-压力-分层关系。提出了一个新的降解功能,将压力-反应和对粘合弹性材料的损害演化适当结合起来。我们获得了一套不同的方程,其中考虑到运动、损害和温度的演变。在目前的工作中,为了简单起见,这一模型通过使用半隐含/显性办法,对异热病例进行了数字解。包括实验数据相配的几项数字测试表明,已开发的模型核算对小型和有限菌株的粘合材料损害进行了适当的计算。今后的工作将考虑非热数值模拟。