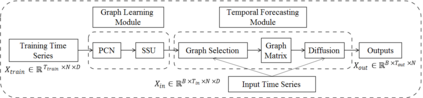
Accurate forecasting of multivariate time series is an extensively studied subject in finance, transportation, and computer science. Fully mining the correlation and causation between the variables in a multivariate time series exhibits noticeable results in improving the performance of a time series model. Recently, some models have explored the dependencies between variables through end-to-end graph structure learning without the need for pre-defined graphs. However, most current models do not incorporate the trade-off between effectiveness and flexibility and lack the guidance of domain knowledge in the design of graph learning algorithms. Besides, they have issues generating sparse graph structures, which pose challenges to end-to-end learning. In this paper, we propose Learning Sparse and Continuous Graphs for Forecasting (LSCGF), a novel deep learning model that joins graph learning and forecasting. Technically, LSCGF leverages the spatial information into convolutional operation and extracts temporal dynamics using the diffusion convolution recurrent network. At the same time, we propose a brand new method named Smooth Sparse Unit (SSU) to learn sparse and continuous graph adjacency matrix. Extensive experiments on three real-world datasets demonstrate that our model achieves state-of-the-art performances with minor trainable parameters.
翻译:对多变时间序列的准确预测是金融、交通和计算机科学领域广泛研究的一个课题。充分挖掘多变时间序列变量之间的相互关系和因果关系,显示在改善时间序列模型的性能方面取得显著成果。最近,一些模型通过端对端图形结构学习探索了变量之间的相互依存性,而不需要预先界定的图表结构学习。然而,大多数目前的模型没有将有效性和灵活性之间的权衡纳入考虑范围,在设计图表学习算法时缺乏对域知识的指导。此外,它们还存在产生微小的图形结构的问题,对端对端学习构成挑战。在本文件中,我们提出了“预测学粗略和连续图表”(LSCGF),这是一个与图表学习和预测相结合的新的深层次学习模型。技术上,LSCGF将空间信息用于演化操作,并利用扩散共振经常网络提取时间动态。与此同时,我们提出了一种名为“平流”的品牌新方法,以学习零星和连续的相邻图形矩阵。在三个现实世界的模型上进行广泛的实验,用少量数据参数显示我们实现模型的绩效。
相关内容
Source: Apple - iOS 8