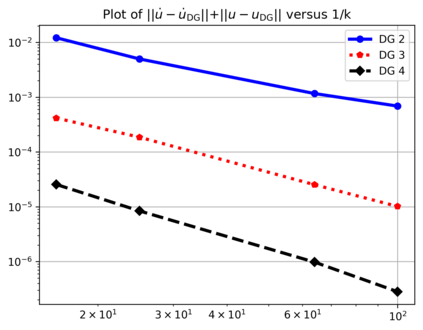
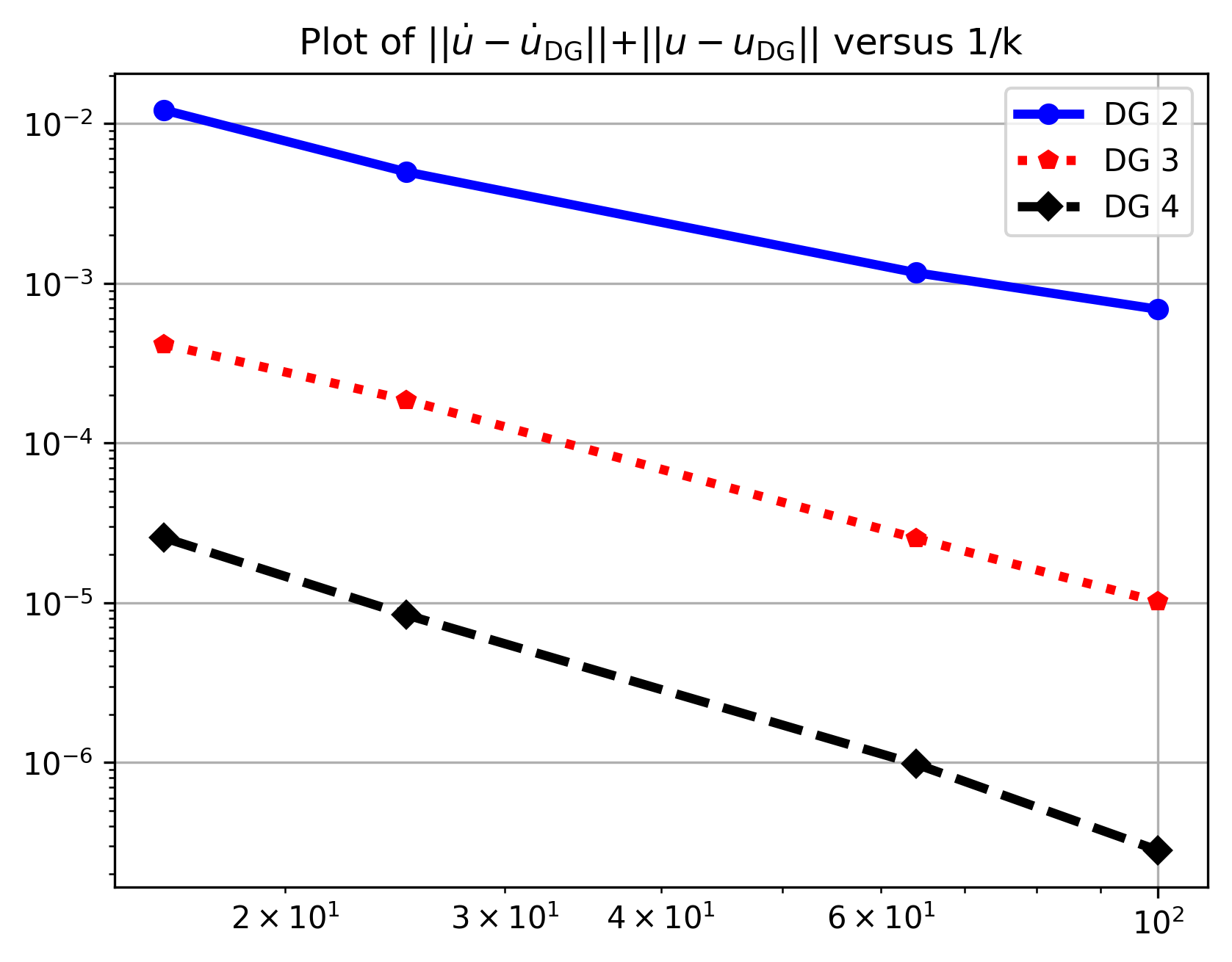
In this paper we study the finite element approximation of systems of second-order nonlinear hyperbolic equations. The proposed numerical method combines a $hp$-version discontinuous Galerkin finite element approximation in the time direction with an $H^1(\Omega)$-conforming finite element approximation in the spatial variables. Error bounds at the temporal nodal points are derived under a weak restriction on the temporal step size in terms of the spatial mesh size. Numerical experiments are presented to verify the theoretical results.
翻译:在本文中,我们研究了二级非线性双曲方程式系统的有限元素近似值。拟议的数字方法将时间方向的美元-美元反转不连续的加勒金有限元素近近值与空间变量的美元1 (\ OMEGA) 美元与美元一致的有限元素近似值结合起来。时间节点的误差界限是根据对空间网格大小的时阶大小的较弱限制而得出的。提出了数字实验,以核实理论结果。
相关内容
Arxiv
0+阅读 · 2022年2月2日
Arxiv
0+阅读 · 2022年2月2日
Arxiv
0+阅读 · 2022年2月1日