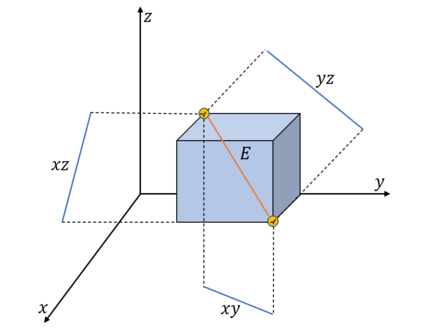
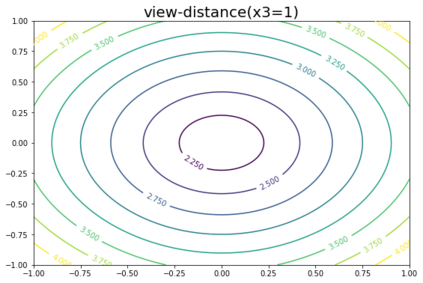
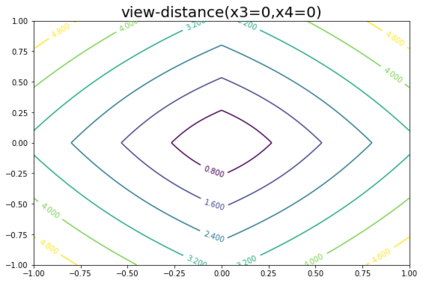
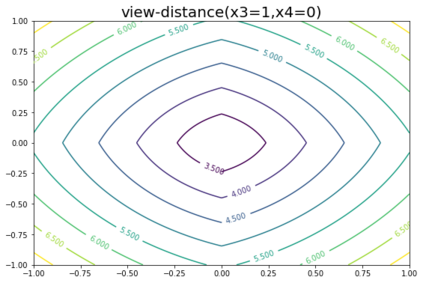
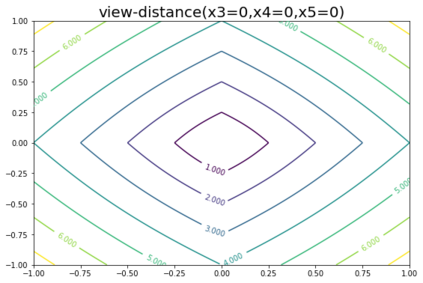
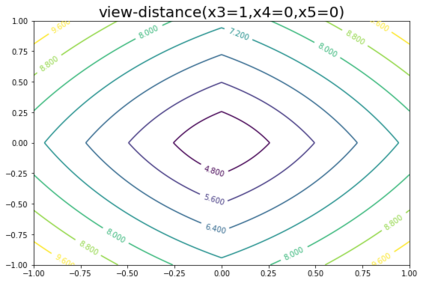
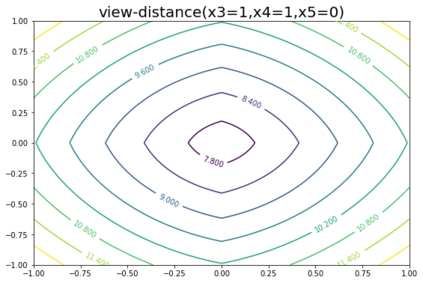
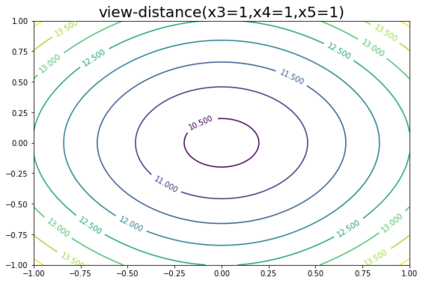
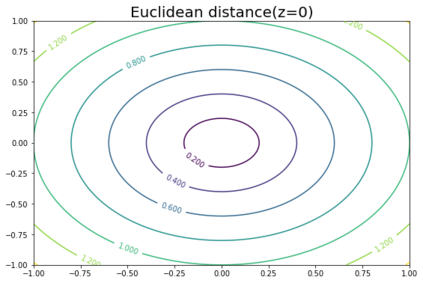
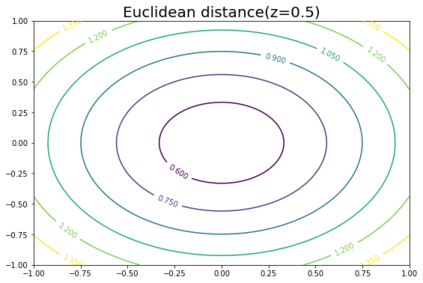
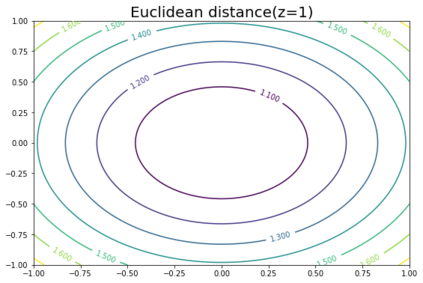
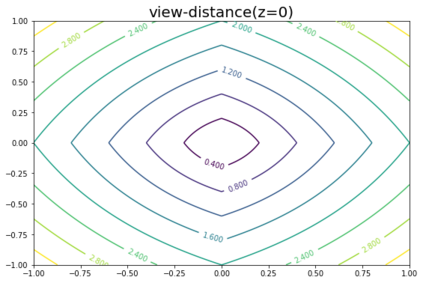
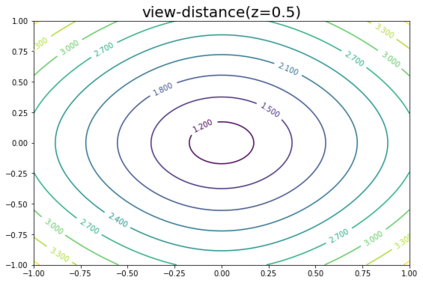
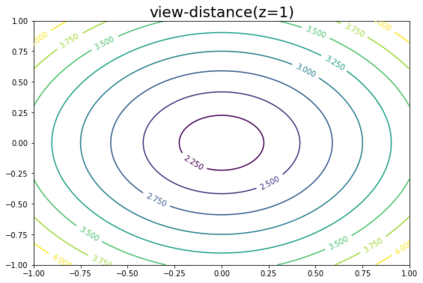
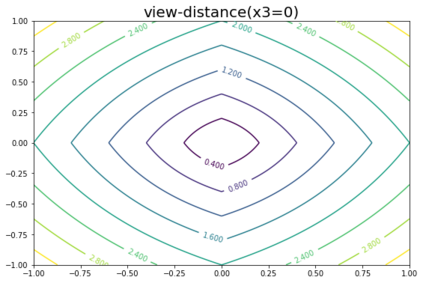
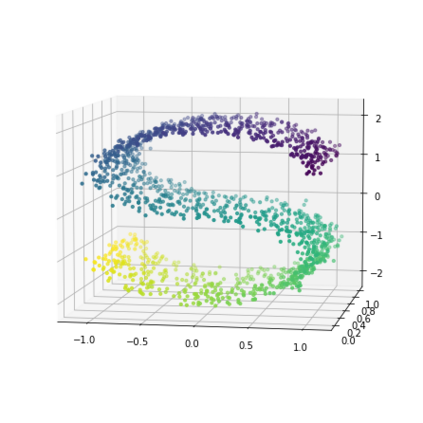
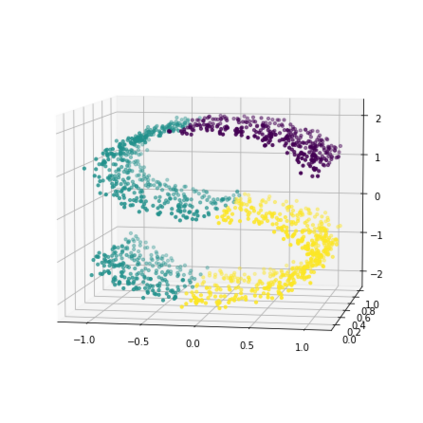
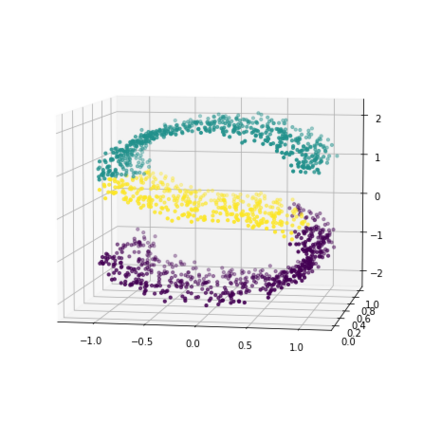
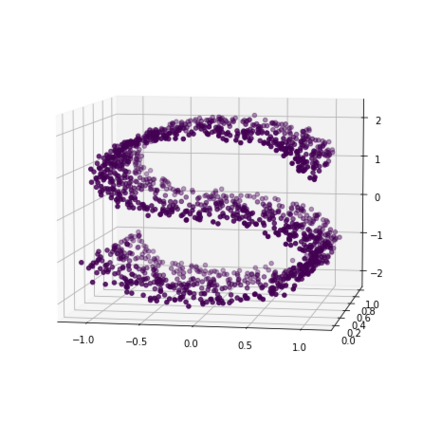
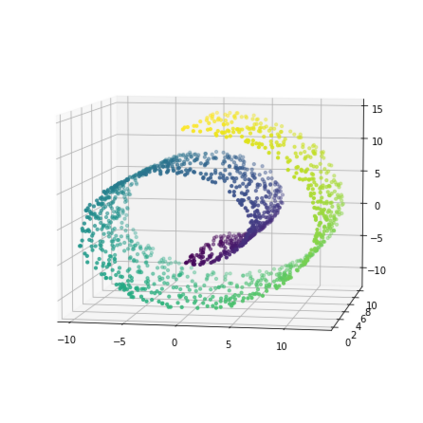
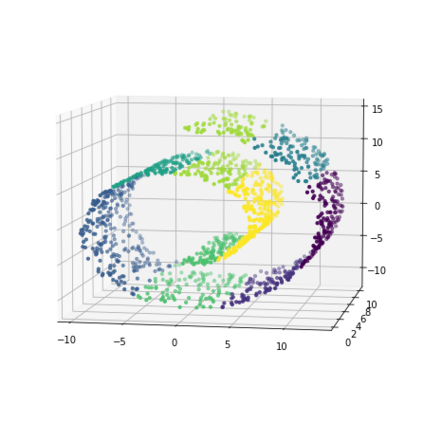
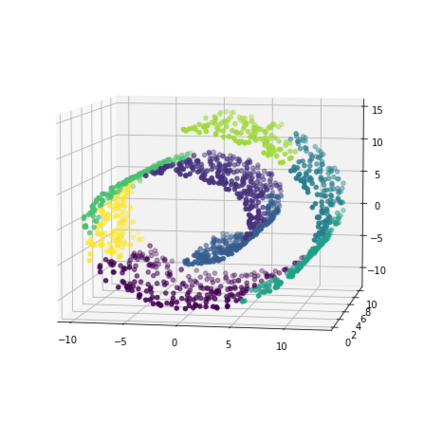
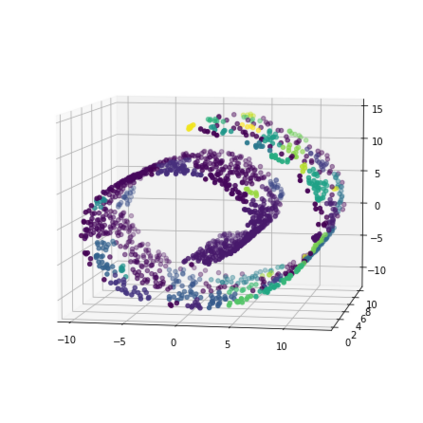
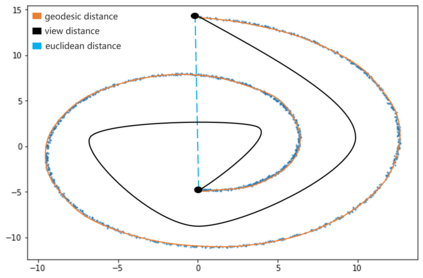
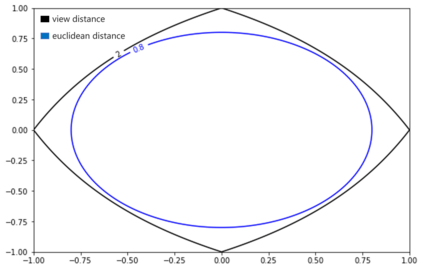
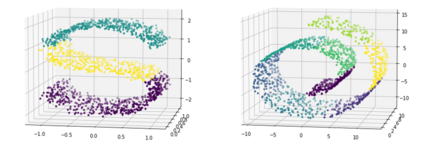
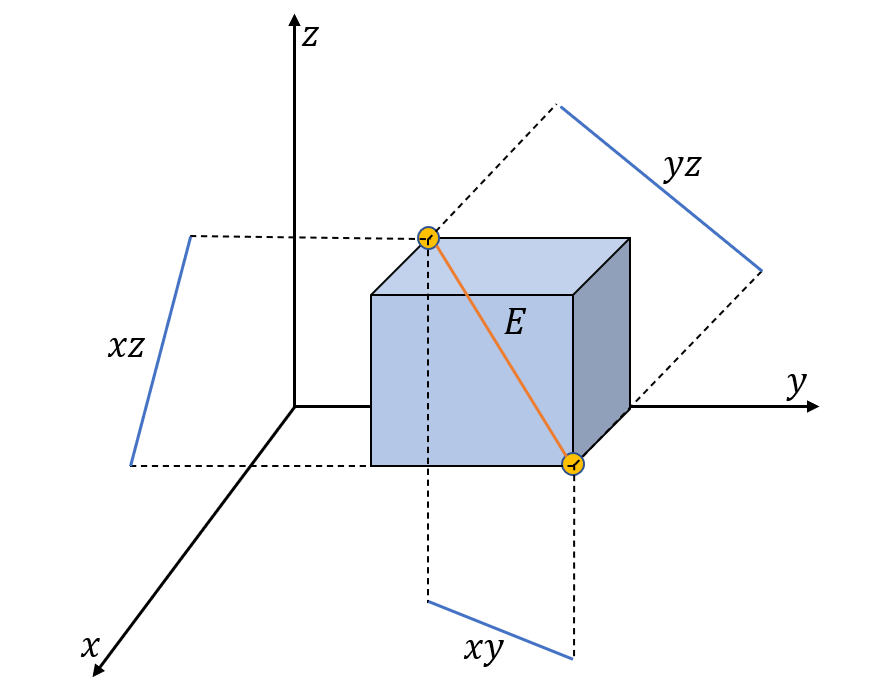
K-Means clustering algorithm is one of the most commonly used clustering algorithms because of its simplicity and efficiency. K-Means clustering algorithm based on Euclidean distance only pays attention to the linear distance between samples, but ignores the overall distribution structure of the dataset (i.e. the fluid structure of dataset). Since it is difficult to describe the internal structure of two data points by Euclidean distance in high-dimensional data space, we propose a new distance measurement, namely, view-distance, and apply it to the K-Means algorithm. On the classical manifold learning datasets, S-curve and Swiss roll datasets, not only this new distance can cluster the data according to the structure of the data itself, but also the boundaries between categories are neat dividing lines. Moreover, we also tested the classification accuracy and clustering effect of the K-Means algorithm based on view-distance on some real-world datasets. The experimental results show that, on most datasets, the K-Means algorithm based on view-distance has a certain degree of improvement in classification accuracy and clustering effect.
翻译:K- Means 群集算法由于其简单性和效率而是最常用的群集算法之一。 K- Means 群集算法仅关注样本之间的线性距离,却忽略了数据集的总体分布结构(即数据集的流体结构 ) 。 由于很难用高维数据空间的 Euclidean 距离来描述两个数据点的内部结构, 我们提议一种新的距离测量法, 即查看距离, 并将其应用到 K- Means 算法中。 在典型的多元学习数据集、 S- 曲线和瑞士滚动数据集中, 不仅这一新距离可以按照数据本身的结构来组合数据, 而且类别之间的界限是整齐的分隔线 。 此外, 我们还测试了K- Means 算法基于一些真实世界数据集的视距的分类准确性和组合效应。 实验结果表明, 在大多数数据集中, 基于视觉距离的K- Means 算法在分类和组合效果方面有一定程度的改进。