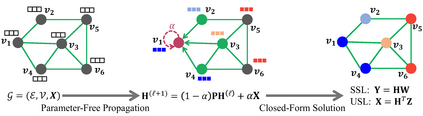
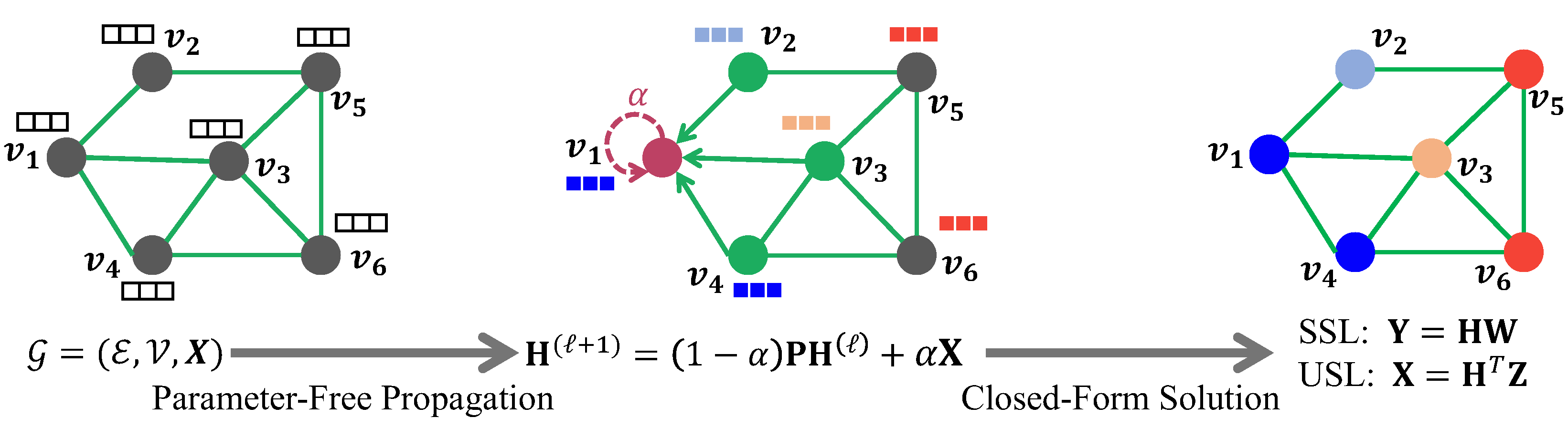
This paper presents FLGC, a simple yet effective fully linear graph convolutional network for semi-supervised and unsupervised learning. Instead of using gradient descent, we train FLGC based on computing a global optimal closed-form solution with a decoupled procedure, resulting in a generalized linear framework and making it easier to implement, train, and apply. We show that (1) FLGC is powerful to deal with both graph-structured data and regular data, (2) training graph convolutional models with closed-form solutions improve computational efficiency without degrading performance, and (3) FLGC acts as a natural generalization of classic linear models in the non-Euclidean domain, e.g., ridge regression and subspace clustering. Furthermore, we implement a semi-supervised FLGC and an unsupervised FLGC by introducing an initial residual strategy, enabling FLGC to aggregate long-range neighborhoods and alleviate over-smoothing. We compare our semi-supervised and unsupervised FLGCs against many state-of-the-art methods on a variety of classification and clustering benchmarks, demonstrating that the proposed FLGC models consistently outperform previous methods in terms of accuracy, robustness, and learning efficiency. The core code of our FLGC is released at https://github.com/AngryCai/FLGC.
翻译:本文介绍FLGC,这是一个简单而有效的半监督和不受监督的半监督和非监督学习完全线性图像革命网络。我们不是使用梯度下降,而是用一个分离程序来计算一种全球最佳封闭式解决方案,从而形成一个普遍的线性框架,更容易实施、培训和应用。我们显示:(1) FLGC具有处理图形结构数据和定期数据的强大能力,(2) 具有封闭式解决方案的培训图像共变模型,可以提高计算效率,而不会降低性能;(3) FLGC作为非欧洲克利德兰域经典线性模型的自然概括化,例如,山脊回归和子空间集群。此外,我们实施一个半封闭式的FLGC和未受监督的FLGC,通过引入初步残余战略,使FLGC能够汇总长程相邻,减轻超移动。我们将我们的半超超度和未超度FLGC模型与许多非欧洲克利德域域域域域域的经典线性模型,例如,山脊回归和子空间集群组合。此外,我们实施一个半受监督的FGC/CL的分类/组合法系的分类和组合法系的可靠核心标准,表明我们先前的FGC/CL的分类和分类和分类法的可靠性能的分类和组合法。