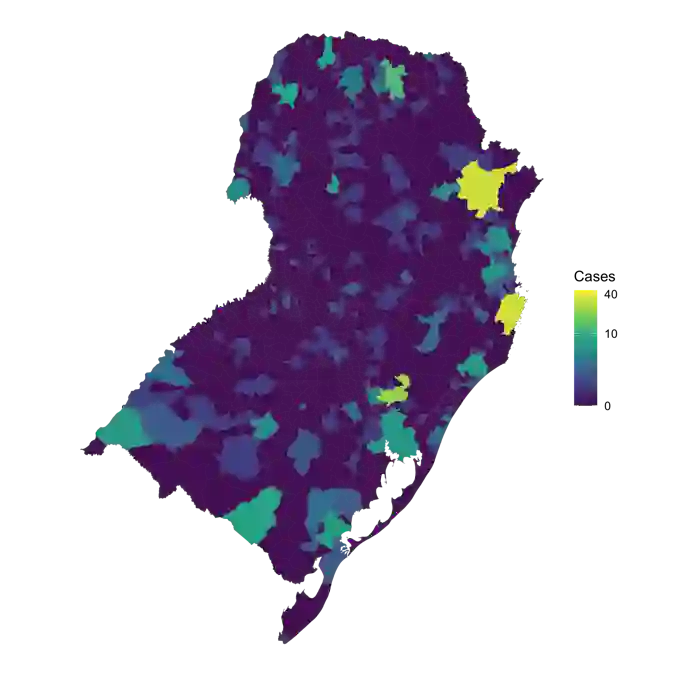
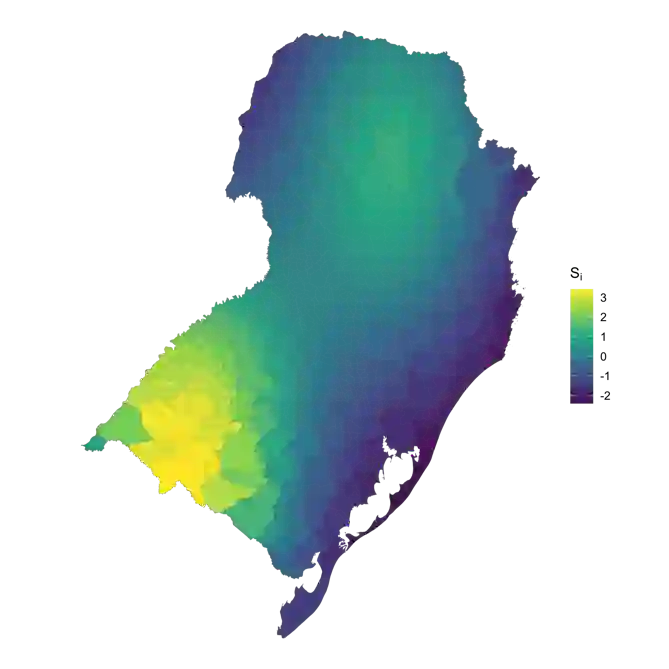
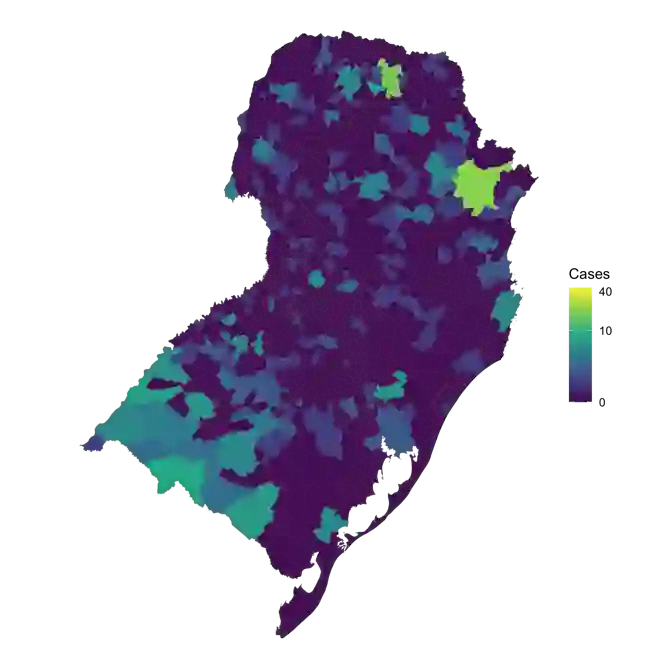
Spatial connectivity is an important consideration when modelling infectious disease data across a geographical region. Connectivity can arise for many reasons, including shared characteristics between regions, and human or vector movement. Bayesian hierarchical models include structured random effects to account for spatial connectivity. However, conventional approaches require the spatial structure to be fully defined prior to model fitting. By applying penalised smoothing splines to coordinates, we create 2-dimensional smooth surfaces describing the spatial structure of the data whilst making minimal assumptions about the structure. The result is a non-stationary surface which is setting specific. These surfaces can be incorporated into a hierarchical modelling framework and interpreted similarly to traditional random effects. Through simulation studies we show that the splines can be applied to any continuous connectivity measure, including measures of human movement, and that the models can be extended to explore multiple sources of spatial structure in the data. Using Bayesian inference and simulation, the relative contribution of each spatial structure can be computed and used to generate hypotheses about the drivers of disease. These models were found to perform at least as well as existing modelling frameworks, whilst allowing for future extensions and multiple sources of spatial connectivity.
翻译:在制作跨地理区域传染病数据模型时,空间连通性是一个重要的考虑因素。由于许多原因,连通性可能出现,包括区域之间共有的特点,以及人类或病媒的移动。贝叶斯等级模型包括结构随机效应,以顾及空间连通性。然而,常规方法要求在模型安装之前充分界定空间结构。通过对坐标应用惩罚性平滑样条,我们创建了描述数据空间结构的二维平滑表面,同时对结构作出最低限度的假设。结果是一个非静止的表层,该表层是具体的。这些表层可以纳入一个等级建模框架,并作类似传统随机效应的解释。通过模拟研究,我们显示这些样条可以适用于任何连续连通性测量,包括人类移动测量,这些模型可以扩展,以探索数据中空间结构的多种来源。利用贝伊斯的推断和模拟,可以计算并使用每种空间结构的相对贡献来产生关于疾病驱动因素的假设。这些模型至少可以运行现有的建模框架,同时允许未来的扩展和空间连通性多种来源。