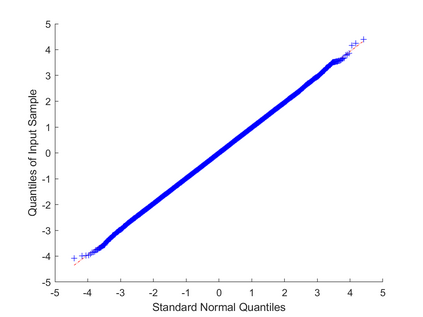
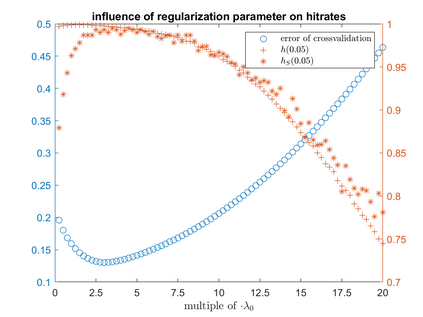
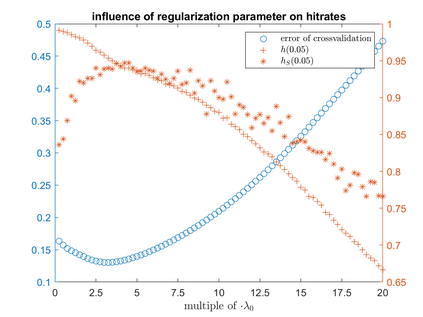
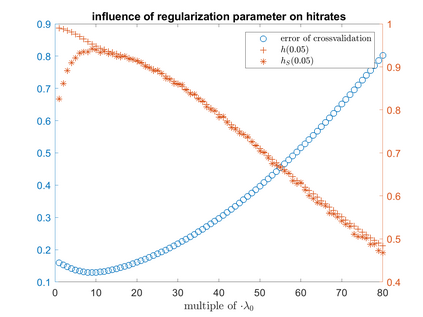
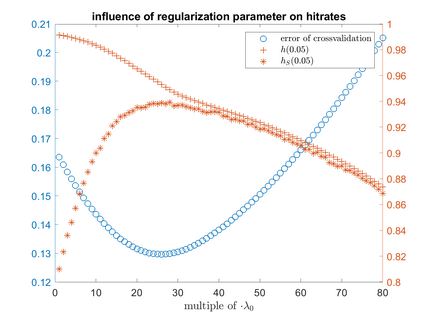
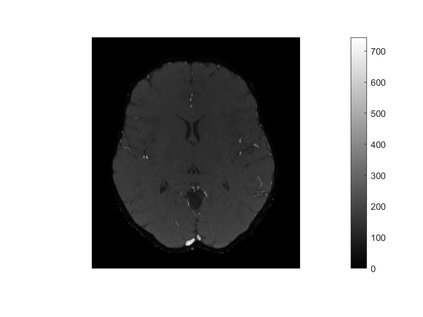
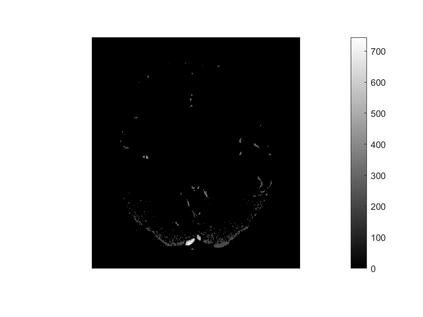
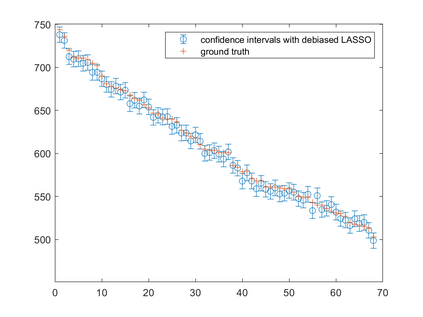
One of the most prominent methods for uncertainty quantification in high-dimen-sional statistics is the desparsified LASSO that relies on unconstrained $\ell_1$-minimization. The majority of initial works focused on real (sub-)Gaussian designs. However, in many applications, such as magnetic resonance imaging (MRI), the measurement process possesses a certain structure due to the nature of the problem. The measurement operator in MRI can be described by a subsampled Fourier matrix. The purpose of this work is to extend the uncertainty quantification process using the desparsified LASSO to design matrices originating from a bounded orthonormal system, which naturally generalizes the subsampled Fourier case and also allows for the treatment of the case where the sparsity basis is not the standard basis. In particular we construct honest confidence intervals for every pixel of an MR image that is sparse in the standard basis provided the number of measurements satisfies $n \gtrsim\max\{ s\log^2 s\log p, s \log^2 p \}$ or that is sparse with respect to the Haar Wavelet basis provided a slightly larger number of measurements.
翻译:高二星统计中最突出的不确定性量化方法之一是利用未受限制的美元=ell_1美元-最小化的LASSO淡化的LASSO。 最初的工程大多侧重于真实的( sub- sub- gausian) 设计。 但是,在许多应用中,例如磁共振成像(MRI),测量过程由于问题的性质而具有某种结构。 MRI 中的测量操作员可以通过分样的 Fleier 矩阵来描述。 这项工作的目的是将不确定性量化进程扩大, 利用已破解的LASSO 设计来自受约束的正统系统的信息矩阵, 该系统自然地将次级抽样的四面体标本案件概括化, 并允许在宽度基础不是标准基础的情况下对案件进行处理。 特别是, 我们为在标准基础中稀疏少的每张MR图像的像像类建立诚实的信任间隔, 提供符合 $\ gtrsimm\ max s\ max\log2 slog2 slog p, srlog2 prgle=2 prgrgle=pleas swabarnal as tostal