Ensemble of Loss Functions to Improve Generalizability of Deep Metric Learning methods

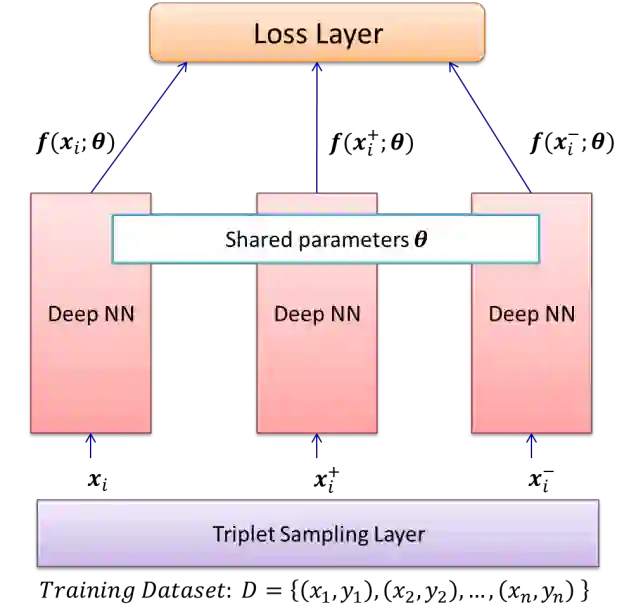
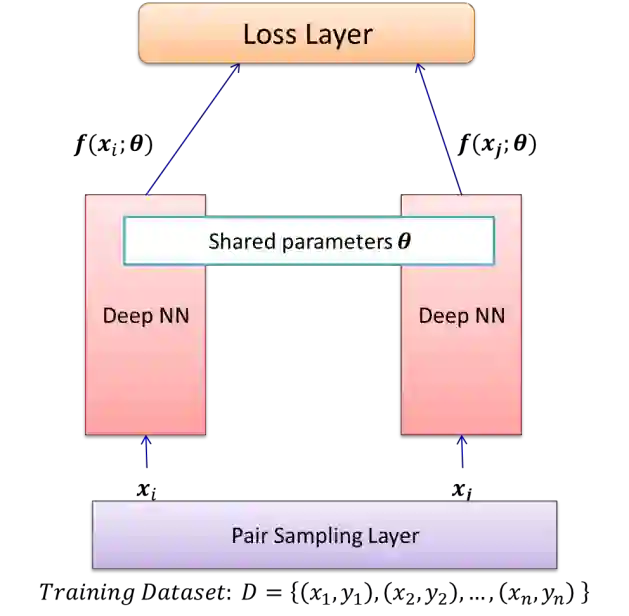
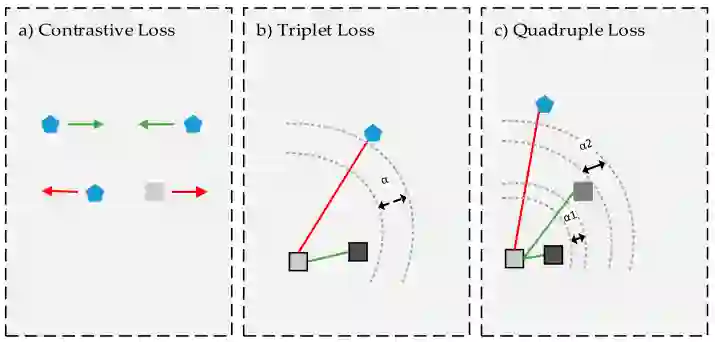
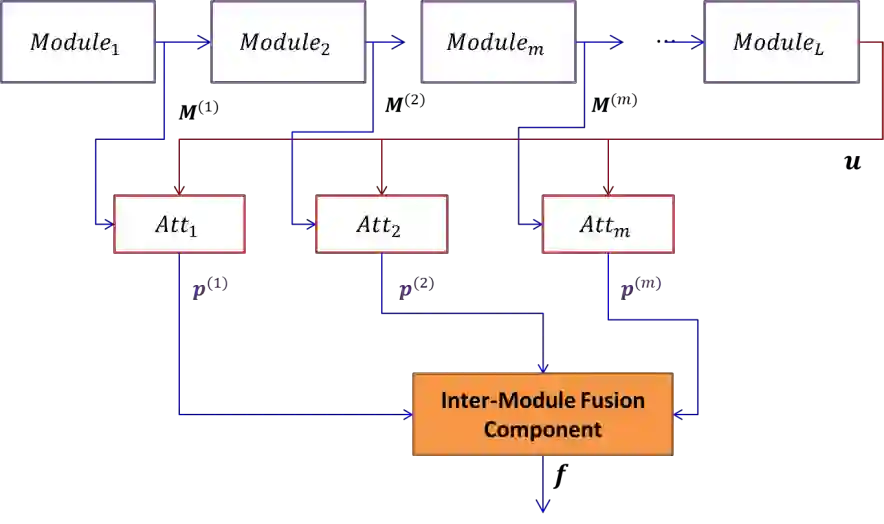
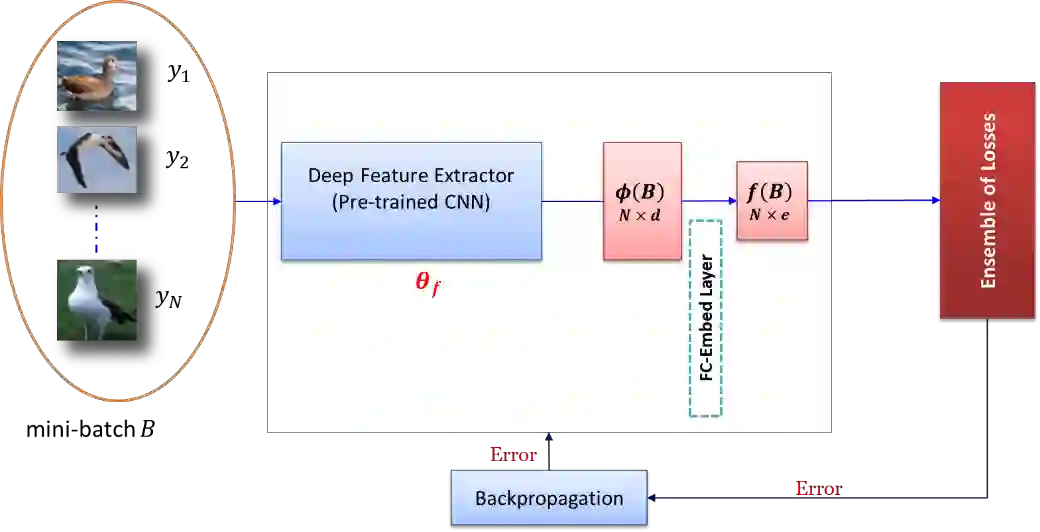
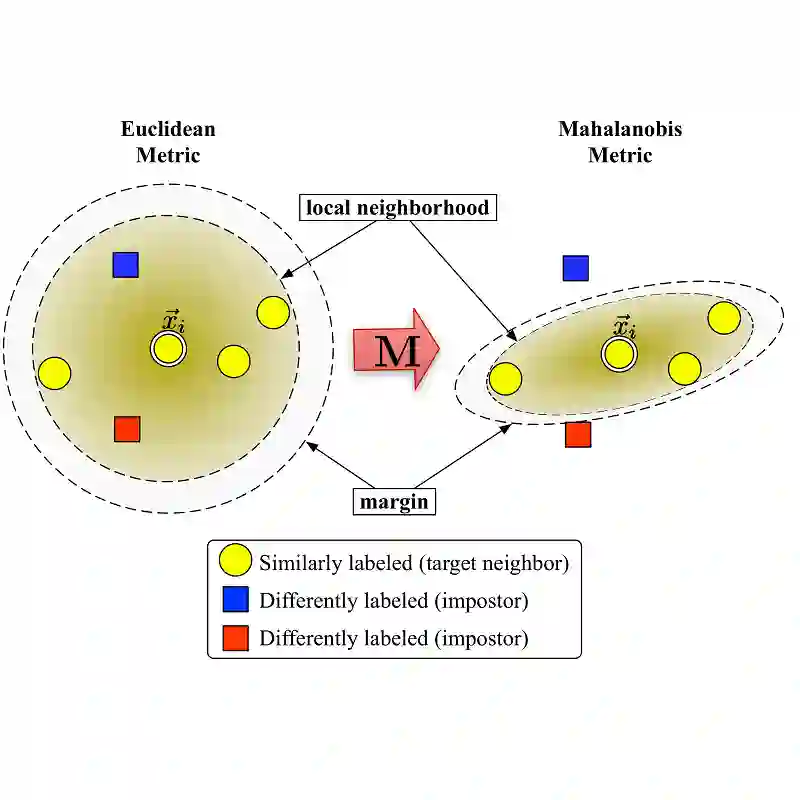
Deep Metric Learning (DML) learns a non-linear semantic embedding from input data that brings similar pairs together while keeps dissimilar data away from each other. To this end, many different methods are proposed in the last decade with promising results in various applications. The success of a DML algorithm greatly depends on its loss function. However, no loss function is perfect, and it deals only with some aspects of an optimal similarity embedding. Besides, the generalizability of the DML on unseen categories during the test stage is an important matter that is not considered by existing loss functions. To address these challenges, we propose novel approaches to combine different losses built on top of a shared deep feature extractor. The proposed ensemble of losses enforces the deep model to extract features that are consistent with all losses. Since the selected losses are diverse and each emphasizes different aspects of an optimal semantic embedding, our effective combining methods yield a considerable improvement over any individual loss and generalize well on unseen categories. Here, there is no limitation in choosing loss functions, and our methods can work with any set of existing ones. Besides, they can optimize each loss function as well as its weight in an end-to-end paradigm with no need to adjust any hyper-parameter. We evaluate our methods on some popular datasets from the machine vision domain in conventional Zero-Shot-Learning (ZSL) settings. The results are very encouraging and show that our methods outperform all baseline losses by a large margin in all datasets.