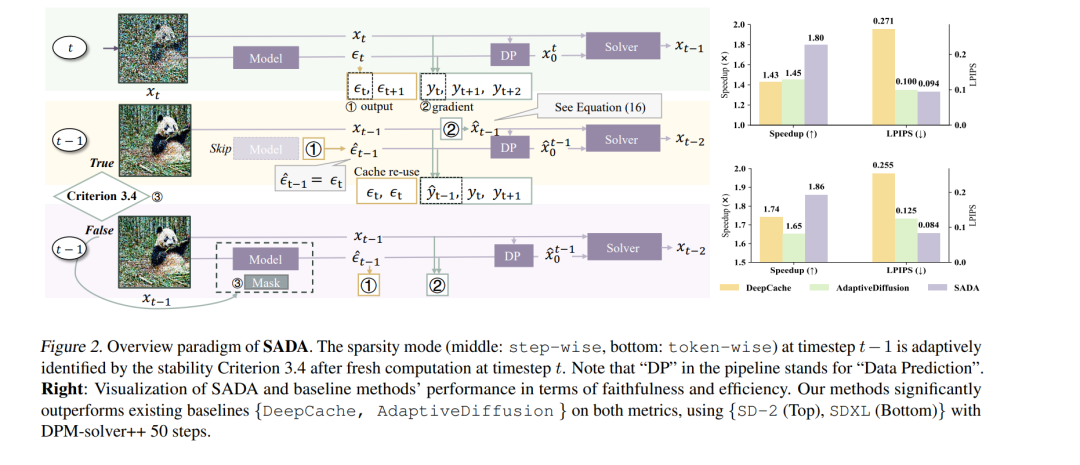
扩散模型在生成任务中取得了显著成功,但由于其迭代采样过程和二次复杂度的注意力机制,计算成本较高。现有的免训练加速策略通过降低每步计算开销,虽在减少采样时间方面表现有效,却相较于原始基线在保真度上存在明显差距。我们认为这一保真度差距源于:(a) 不同的提示词对应不同的去噪轨迹;(b) 此类方法未考虑扩散过程背后的常微分方程(ODE)建模及其数值解法。 为此,我们提出了一种新颖的加速范式——稳定性引导的自适应扩散加速(SADA),该方法通过统一的稳定性判据,将逐步稀疏性与逐 token 稀疏性决策融合,用于加速基于 ODE 的生成模型(如扩散模型与流匹配模型)的采样过程。针对问题 (a),SADA 能依据采样轨迹自适应地分配稀疏度;针对问题 (b),SADA 引入了基于数值 ODE 求解器的精确梯度信息,设计了有理论依据的近似方案。 我们在 SD-2、SDXL 和 Flux 上,使用 EDM 与 DPM++ 求解器对 SADA 进行了全面评估。结果显示,在几乎不损失保真度(以 LPIPS 和 FID 度量)的前提下,SADA 实现了稳定的加速效果,并显著优于现有方法。此外,SADA 可无缝适配其他推理流程与模态:它无需任何修改即可加速 ControlNet,并能在 MusicLDM 中实现加速,同时保持频谱图 LPIPS 表现优异。
成为VIP会员查看完整内容
相关内容
Arxiv
40+阅读 · 2023年4月19日
Arxiv
81+阅读 · 2023年4月4日
Arxiv
17+阅读 · 2017年12月12日