Eigenvector centrality for multilayer networks with dependent node importance

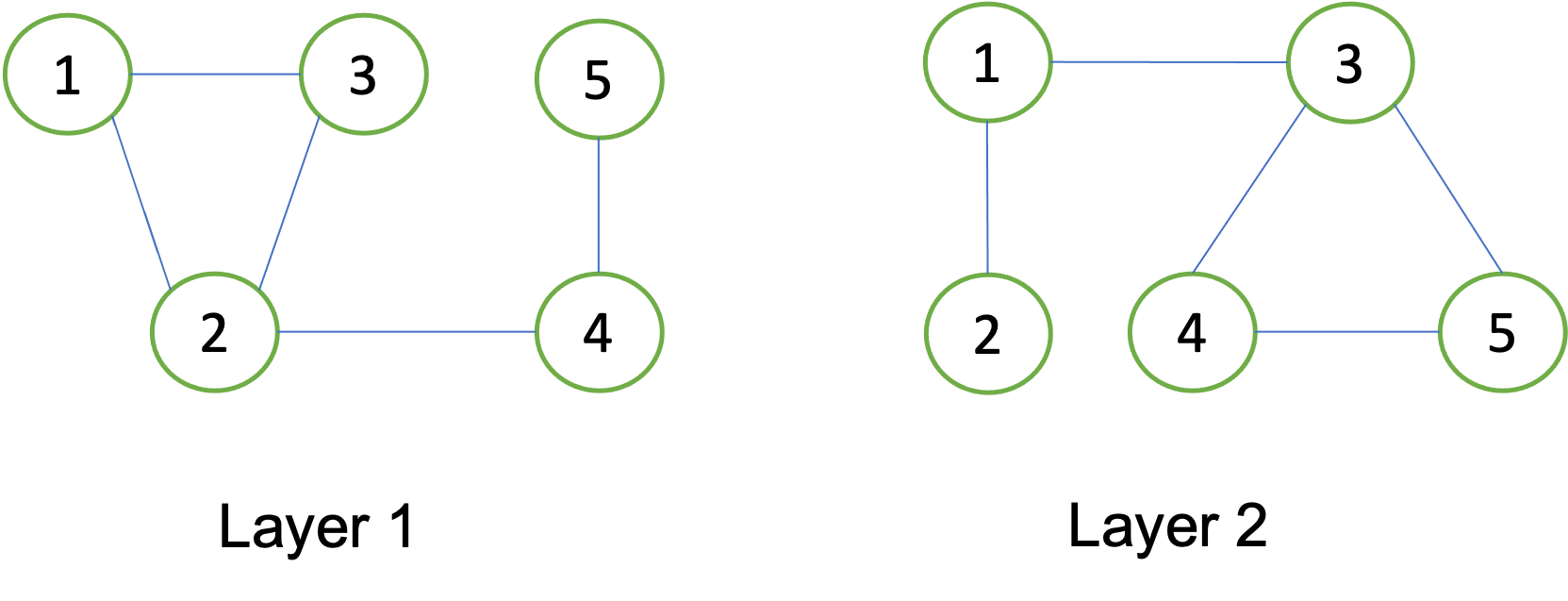
We present an approach for computing eigenvector centrality for multilayer networks with interlayer constraints on node importance. Specifically, we consider a multilayer network defined by multiple edge-weighted, potentially directed, graphs over the same set of nodes with each graph representing one layer of the network. In this scenario, edges between layers are not allowed. As in the standard eigenvector centrality construction, the importance each node in a given layer is based on the weighted sum of the importance of adjacent nodes in that same layer. Unlike standard eigenvector centrality, we assume that the adjacency relationship and the importance of adjacent nodes may be based on distinct layers. This form of centrality constraint between the layers leads to eigenvector centrality values defined by a system of interdependent eigenvalue problems, whose solution can be efficiently realized using an interleaved power iteration algorithm.