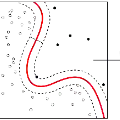
Most anomaly detection (AD) models are learned using only normal samples in an unsupervised way, which may result in ambiguous decision boundary and insufficient discriminability. In fact, a few anomaly samples are often available in real-world applications, the valuable knowledge of known anomalies should also be effectively exploited. However, utilizing a few known anomalies during training may cause another issue that the model may be biased by those known anomalies and fail to generalize to unseen anomalies. In this paper, we tackle supervised anomaly detection, i.e., we learn AD models using a few available anomalies with the objective to detect both the seen and unseen anomalies. We propose a novel explicit boundary guided semi-push-pull contrastive learning mechanism, which can enhance model's discriminability while mitigating the bias issue. Our approach is based on two core designs: First, we find an explicit and compact separating boundary as the guidance for further feature learning. As the boundary only relies on the normal feature distribution, the bias problem caused by a few known anomalies can be alleviated. Second, a boundary guided semi-push-pull loss is developed to only pull the normal features together while pushing the abnormal features apart from the separating boundary beyond a certain margin region. In this way, our model can form a more explicit and discriminative decision boundary to distinguish known and also unseen anomalies from normal samples more effectively. Code will be available at https://github.com/xcyao00/BGAD.
翻译:大多数异常检测 (AD) 模型都是仅使用正常样本进行无监督学习的方式进行学习的,这可能会导致决策边界的模糊性和不足的可分性。实际上,在现实世界的应用中通常既有正常样本,也有一些异常样本,应该也能有效地利用已知异常的有关知识。然而,在训练期间利用少数已知异常可能会导致另一个问题,即模型可能会受到已知异常的偏见,无法推广到未知的异常。在本文中,我们针对受监督的异常检测进行研究,即我们使用一些可用的异常数据学习 AD 模型,以便检测出未知的异常和已知的异常。我们提出了一种新颖的显性边界引导半推半拉对比学习机制,该机制可以增强模型的可分性同时减轻偏见问题。我们的方法基于两个核心设计:首先,我们找到一个显式且紧凑的分界线作为进一步特征学习的指导。由于分界线仅依赖于正常特征分布,因此可以减轻由少数已知异常引起的偏见问题。其次,我们开发了一种基于边界引导的半推半拉损失,仅将正常特征拉在一起,同时将异常特征推离分界线超出一定的边缘区域。这样,我们的模型可以形成一个更明确和有区分度的决策边界,更有效地区分来自正常样本的已知和未知异常。代码将可以在 https://github.com/xcyao00/BGAD 中找到。