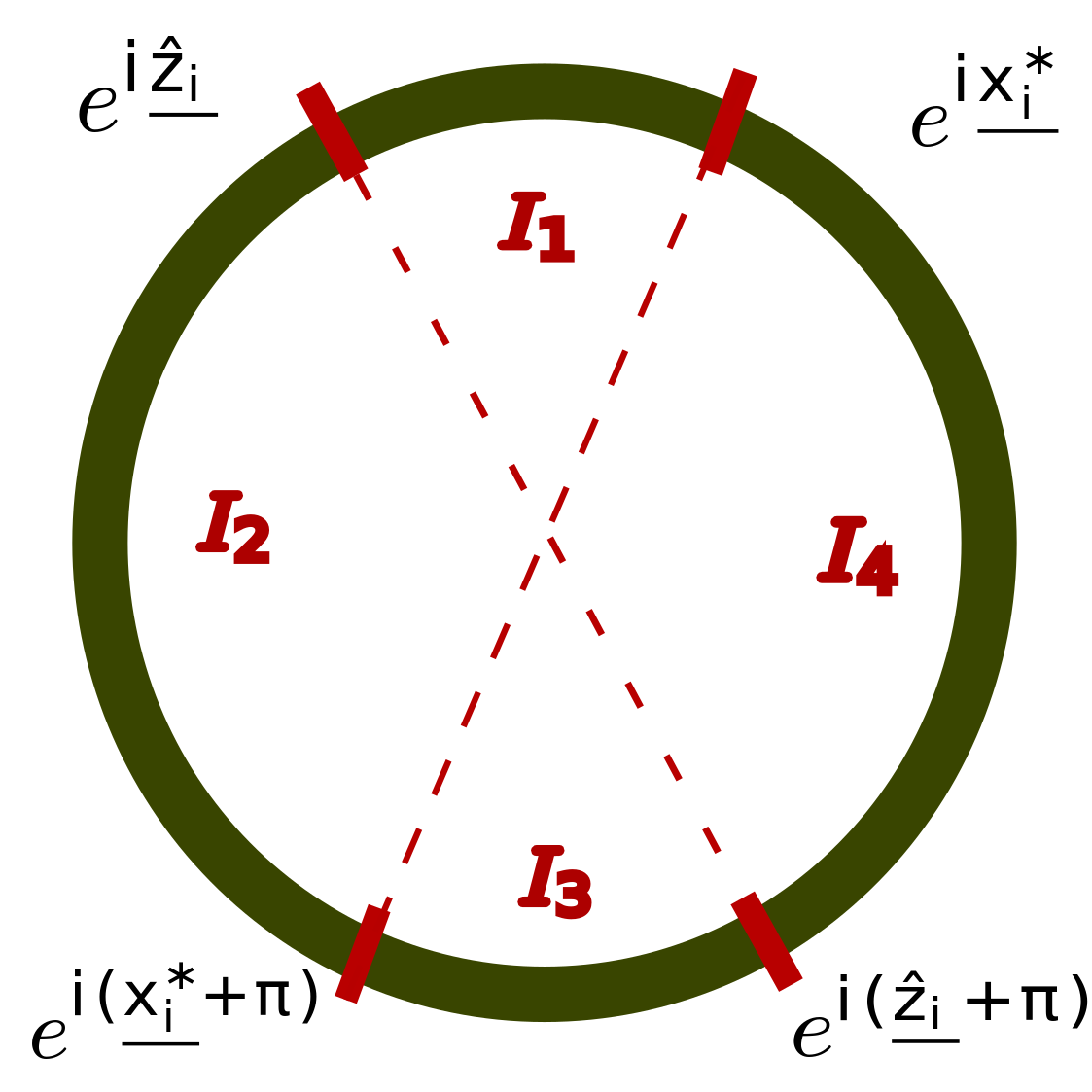
We consider the problem of estimating latent positions in a one-dimensional torus from pairwise affinities. The observed affinity between a pair of items is modeled as a noisy observation of a function $f(x^*_{i},x^*_{j})$ of the latent positions $x^*_{i},x^*_{j}$ of the two items on the torus. The affinity function $f$ is unknown, and it is only assumed to fulfill some shape constraints ensuring that $f(x,y)$ is large when the distance between $x$ and $y$ is small, and vice-versa. This non-parametric modeling offers a good flexibility to fit data. We introduce an estimation procedure that provably localizes all the latent positions with a maximum error of the order of $\sqrt{\log(n)/n}$, with high-probability. This rate is proven to be minimax optimal. A computationally efficient variant of the procedure is also analyzed under some more restrictive assumptions. Our general results can be instantiated to the problem of statistical seriation, leading to new bounds for the maximum error in the ordering.
翻译:我们考虑的是从双亲亲近的角度估计一维面体中潜伏位置的问题。 观察到的一对物品之间的亲近性被模拟为对一个功能( x ⁇ i},x ⁇ j}) 的响亮观测, 以对面体中两个物品的潜在位置( x ⁇ i},x ⁇ j}) $x ⁇ i 美元为代表。 亲近性函数未知, 只是假设它能满足某种形状限制, 以确保当美元与美元之间的距离小时, 美元( x,y) 美元是巨大的, 而反之亦然。 这种非参数模型为适应数据提供了良好的灵活性。 我们引入了一种估算程序, 将所有潜伏位置本地化, 且极有可能发生最大误差的 $sqrt_log(n)/n) 美元 。 这一比率被证明是最小的。 在一些更具限制性的假设下, 对程序的一个具有计算效率的变式也进行了分析。 我们的一般结果可以即刻到统计真实性的问题, 导致在最大误差中进行新的调整。