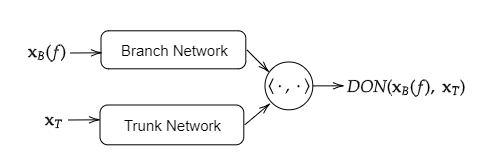
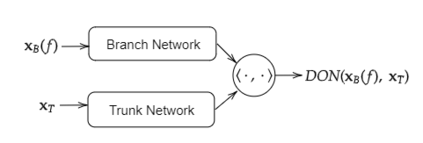
In recent times machine learning methods have made significant advances in becoming a useful tool for analyzing physical systems. A particularly active area in this theme has been "physics informed machine learning" [1] which focuses on using neural nets for numerically solving differential equations. Among all the proposals for solving differential equations using deep-learning, in this paper we aim to advance the theory of generalization error for DeepONets - which is unique among all the available ideas because of its particularly intriguing structure of having an inner-product of two neural nets. Our key contribution is to give a bound on the Rademacher complexity for a large class of DeepONets. Our bound does not explicitly scale with the number of parameters of the nets involved and is thus a step towards explaining the efficacy of overparameterized DeepONets. Additionally, a capacity bound such as ours suggests a novel regularizer on the neural net weights that can help in training DeepONets - irrespective of the differential equation being solved. [1] G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, and L. Yang. Physics-informed machine learning. Nature Reviews Physics, 2021.
翻译:近些年来,机器学习方法在成为分析物理系统的有用工具方面取得了显著进步。这个主题的一个特别活跃的领域是“物理知情的机器学习”[1] [1],重点是利用神经网解决数字解析差异方程。在利用深层学习解决差异方程的所有建议中,我们在本文件中的目标是推进DeepONets的概括性错误理论,这是所有现有想法中独一无二的,因为它拥有两个神经网的内产物这一特别令人感兴趣的结构。我们的主要贡献是,对大型深层ONets的Rademacher复杂性进行约束。我们的界限与所涉网络参数的数目没有明确的规模,因此是朝着解释过分的DeepONets的功效迈出的一步。此外,像我们这样捆绑的能力表明,在神经网重量上有一个新颖的常规化器,可以帮助培训DeepONets -- -- 不论差异方程式正在解决。 [1] G. E. E. E. E. Carniadakis, I. K. G. Kevrekidididid, L. L. L. L. L., Perdikarisal, S. 20, Stal-Iarvieward.