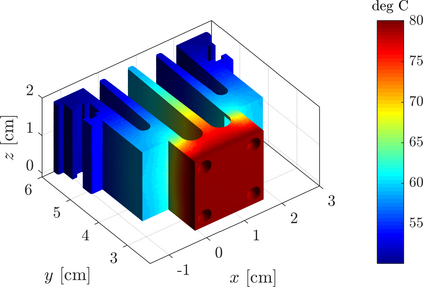
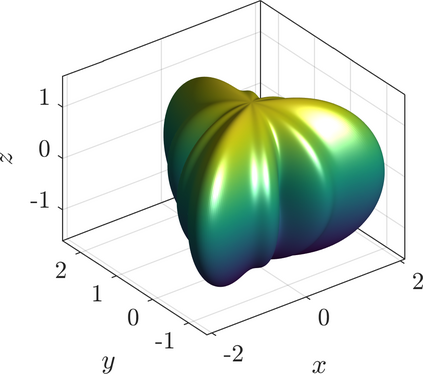
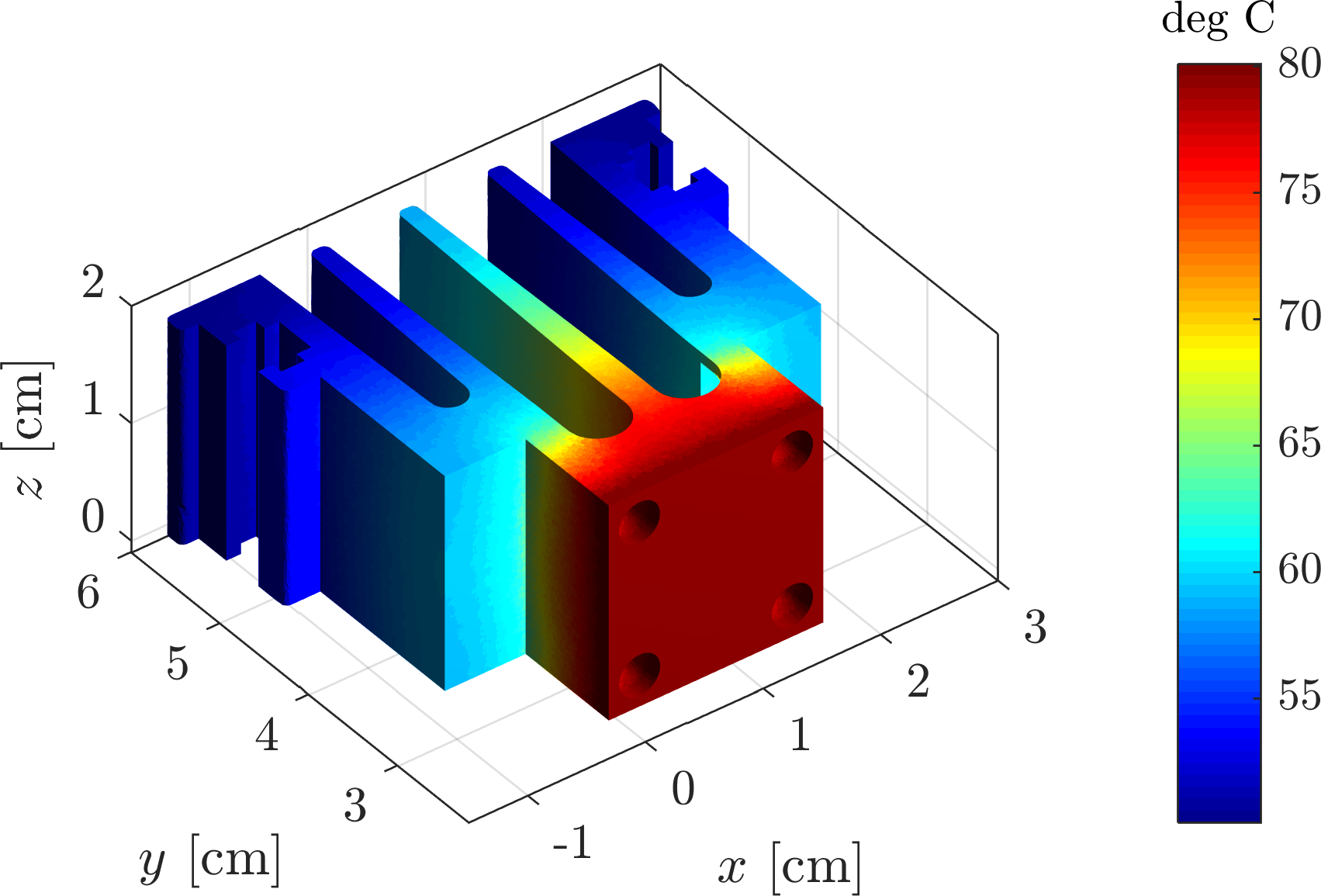
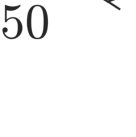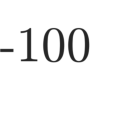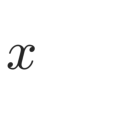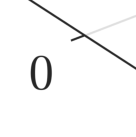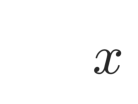In this paper, we present a novel parallel dimension-independent node positioning algorithm that is capable of generating nodes with variable density, suitable for meshless numerical analysis. A very efficient sequential algorithm based on Poisson disc sampling is parallelized for use on shared-memory computers, such as modern workstations with multi-core processors. The parallel algorithm uses a global spatial indexing method with its data divided into two levels, which allows for an efficient multi-threaded implementation. The addition of bootstrapping enables the algorithm to use any number of parallel threads while remaining as general as its sequential variant. We demonstrate the algorithm performance on six complex 2- and 3-dimensional domains, which are either of non-rectangular shape or have varying nodal spacing or both. We perform a run-time analysis of the algorithm, to demonstrate its ability to reach high speedups regardless of the domain and to show how well it scales on the experimental hardware with 16 processor cores. We also analyse the algorithm in terms of the effects of domain shape, quality of point placement, and various parallelization overheads.
翻译:在本文中,我们展示了一种新的平行的维维独立节点定位算法,它能够产生具有可变密度的节点,适合无网点的数值分析。基于 Poisson 盘取样的高效序列算法被平行用于共享的模拟计算机,例如带有多核心处理器的现代工作站。平行算法使用全球空间指数化方法,其数据分为两个层次,从而能够有效地实现多层次的多读执行。加上靴子引线使算法能够使用任何数量的平行线条,同时保持与顺序变异一样的一般。我们展示了6个复合2和3维域的算法性功能,要么是非矩形形状的,要么是不同节点间距或两者兼而有。我们对算法进行了运行时间分析,以显示它无论在哪个领域都能达到高速增长的能力,并展示它如何用16个处理器核心对实验硬件进行缩放。我们还从域形状、点定位质量和各种平行间接结果的角度分析了算法。