Selecting Continuous Life-Like Cellular Automata for Halting Unpredictability: Evolving for Abiogenesis

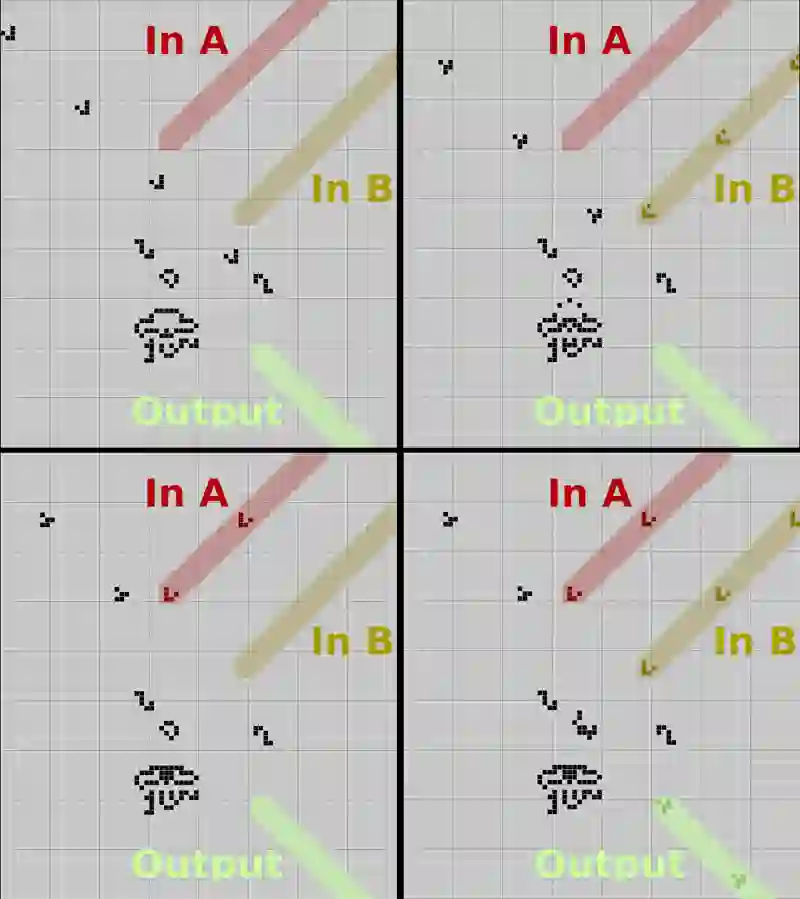
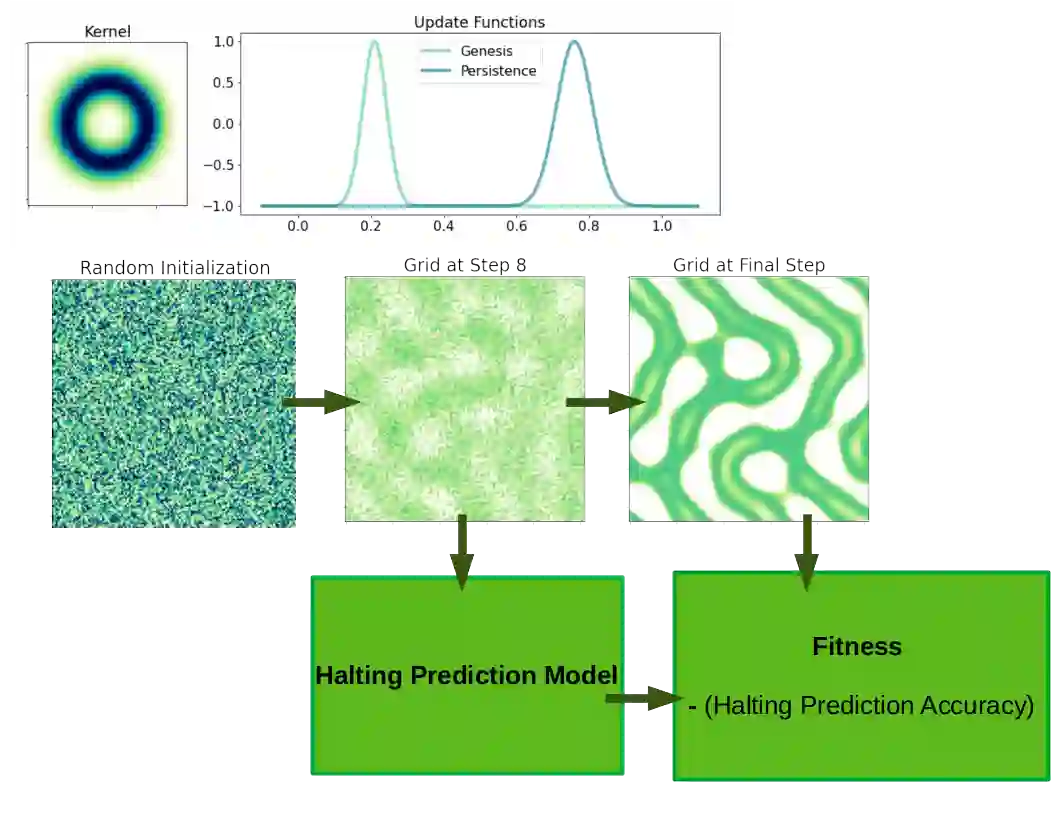
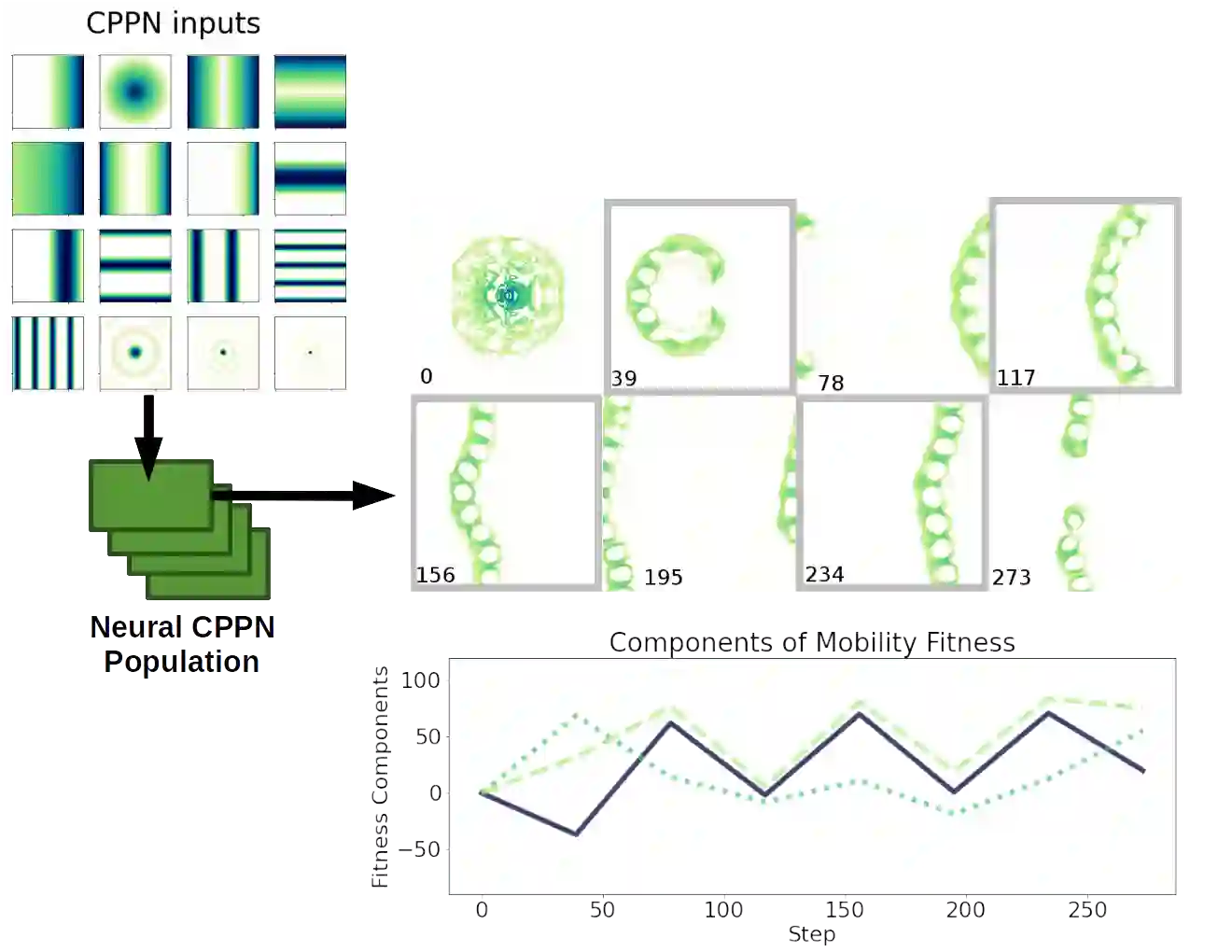
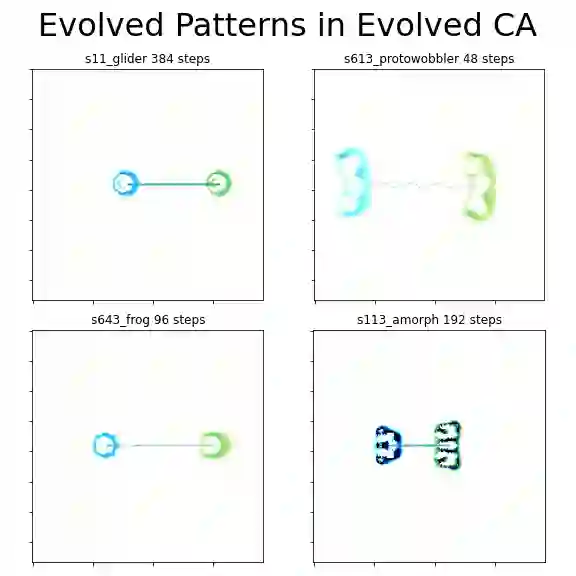
Substantial efforts have been applied to engineer CA with desired emergent properties, such as supporting gliders. Recent work in continuous CA has generated a wide variety of compelling bioreminescent patterns, and the expansion of CA research into continuous numbers, multiple channels, and higher dimensions complicates their study. In this work we devise a strategy for evolving CA and CA patterns in two steps, based on the simple idea that CA are likely to be complex and computationally capable if they support patterns that grow indefinitely as well as patterns that vanish completely, and are difficult to predict the difference in advance. The second part of our strategy evolves patterns by selecting for mobility and conservation of mean cell value. We validate our pattern evolution method by re-discovering gliders in 17 of 17 Lenia CA, and also report 5 new evolved CA that support evolved glider patterns, differing from previously reported Lenia patterns. The CA reported here share neighborhood kernels with previously described Lenia CA, but exhibit a wider range of typical dynamics than their Lenia counterparts. Code for evolving continuous CA is made available under an MIT License.