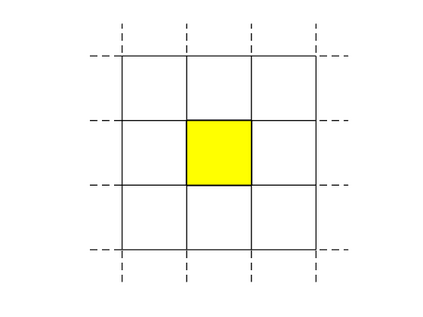
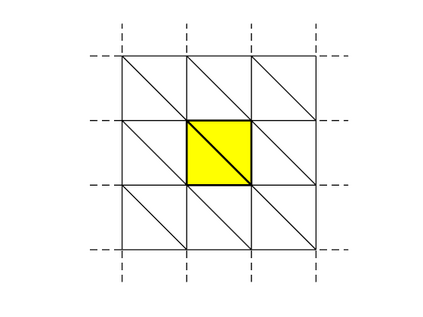
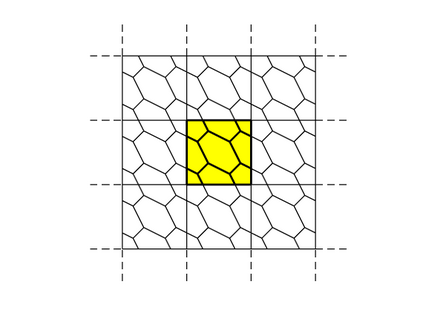
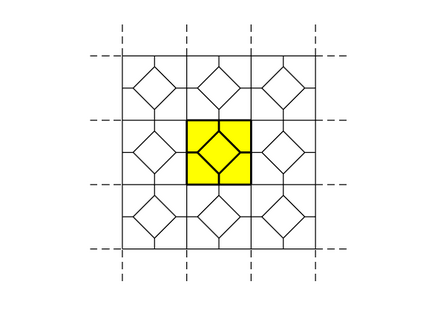
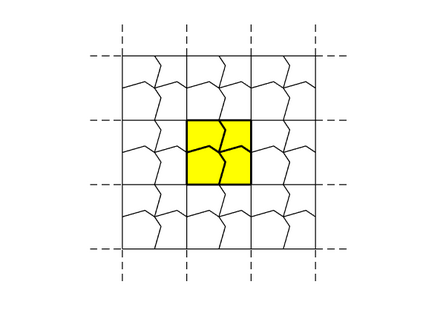
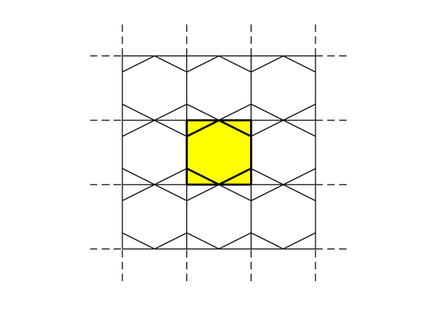
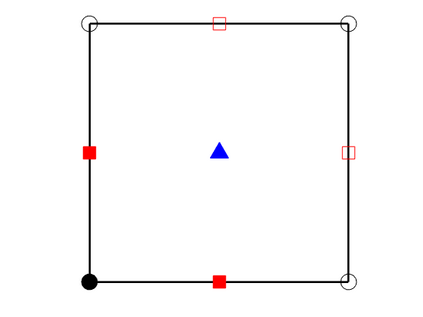
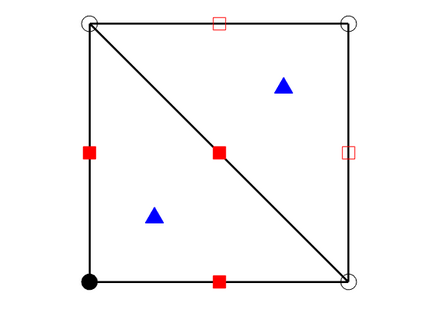
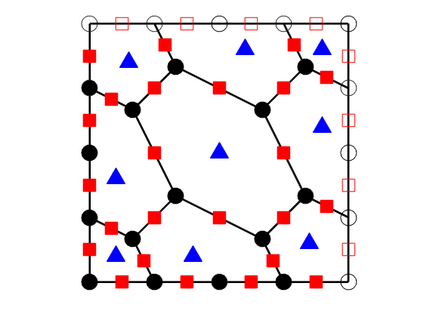
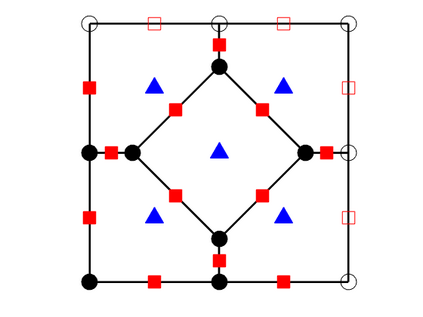
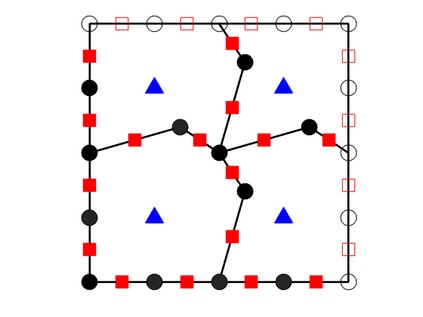
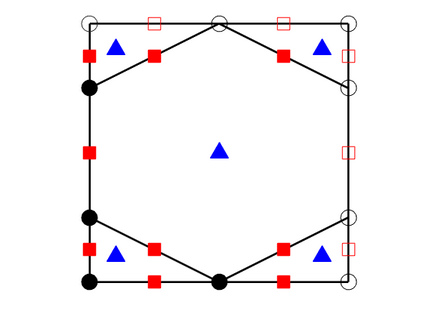
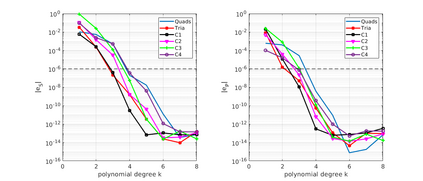
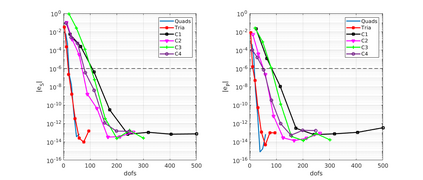
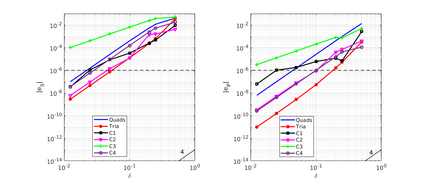
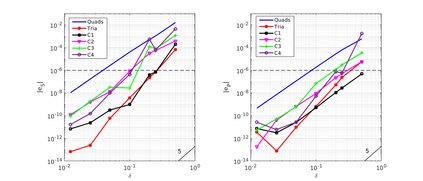
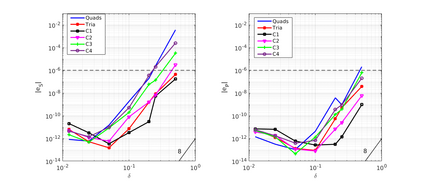
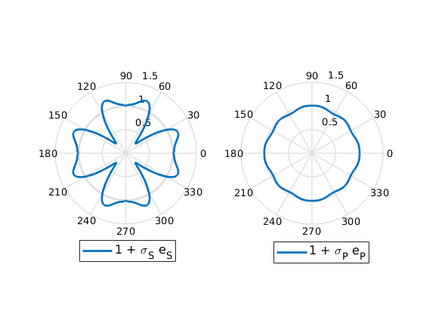
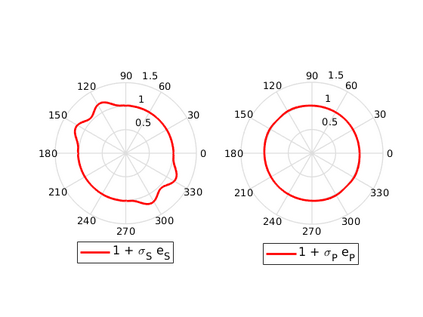
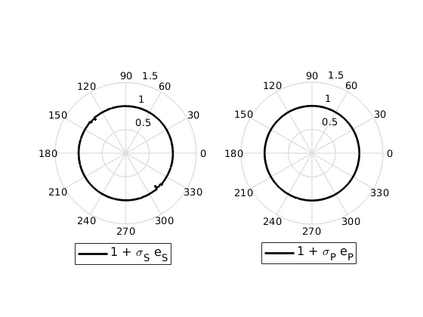
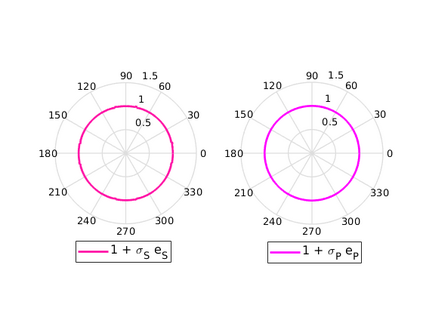
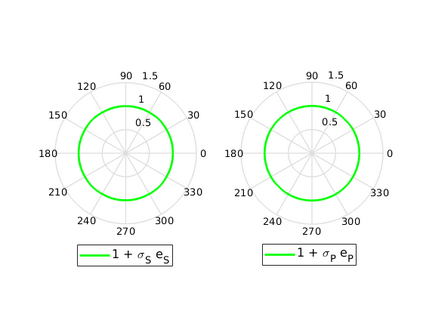
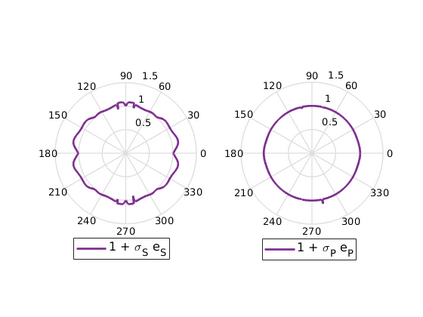
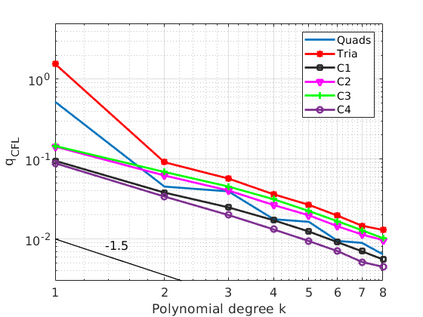
We design the conforming virtual element method for the numerical approximation of the two dimensional elastodynamics problem. We prove stability and convergence of the semi-discrete approximation and derive optimal error estimates under $h$- and $p$-refinement in both the energy and the $L^2$ norms. The performance of the proposed virtual element method is assessed on a set of different computational meshes, including non-convex cells up to order four in the $h$-refinement setting. Exponential convergence is also experimentally observed under p-refinement. Finally, we present a dispersion-dissipation analysis for both the semi-discrete and fully-discrete schemes, showing that polygonal meshes behave as classical simplicial/quadrilateral grids in terms of dispersion-dissipation properties.
翻译:我们设计了符合两个维电子动力学问题数字近似值的虚拟元素方法。我们证明半分解近似值的稳定性和趋同性,并在能量和2美元规范中得出以美元和美元为单位的最佳误差估计值。拟议虚拟元元素方法的性能是通过一套不同的计算模件来评估的,包括非碳化细胞,最多在美元-再精度设置中排列四个。在精炼中也实验性地观测了指数趋同性。最后,我们对半分解和完全分解两种方法都进行了分散性分析,表明多边间藻在分散性特性方面表现为典型的小型/半边际网格。