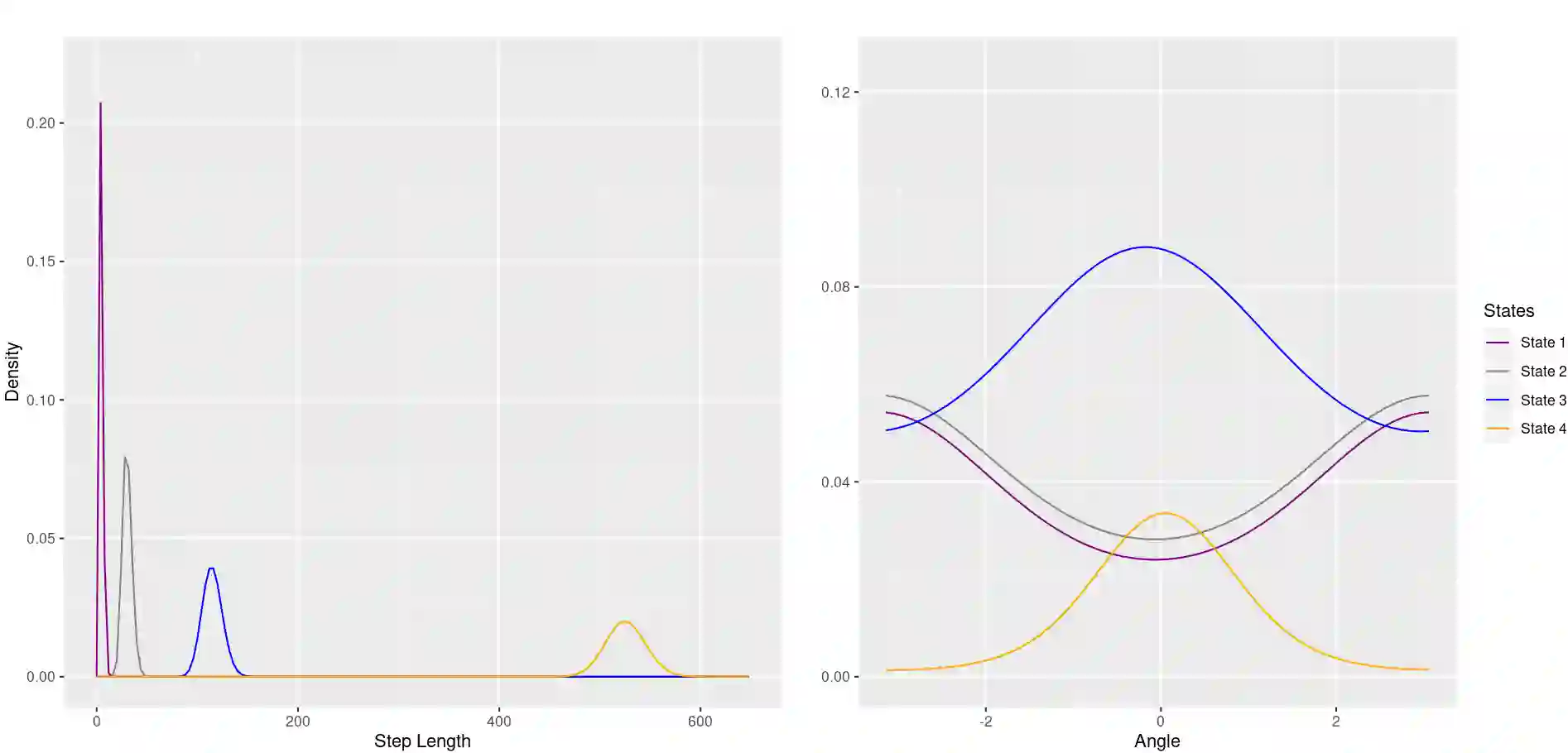
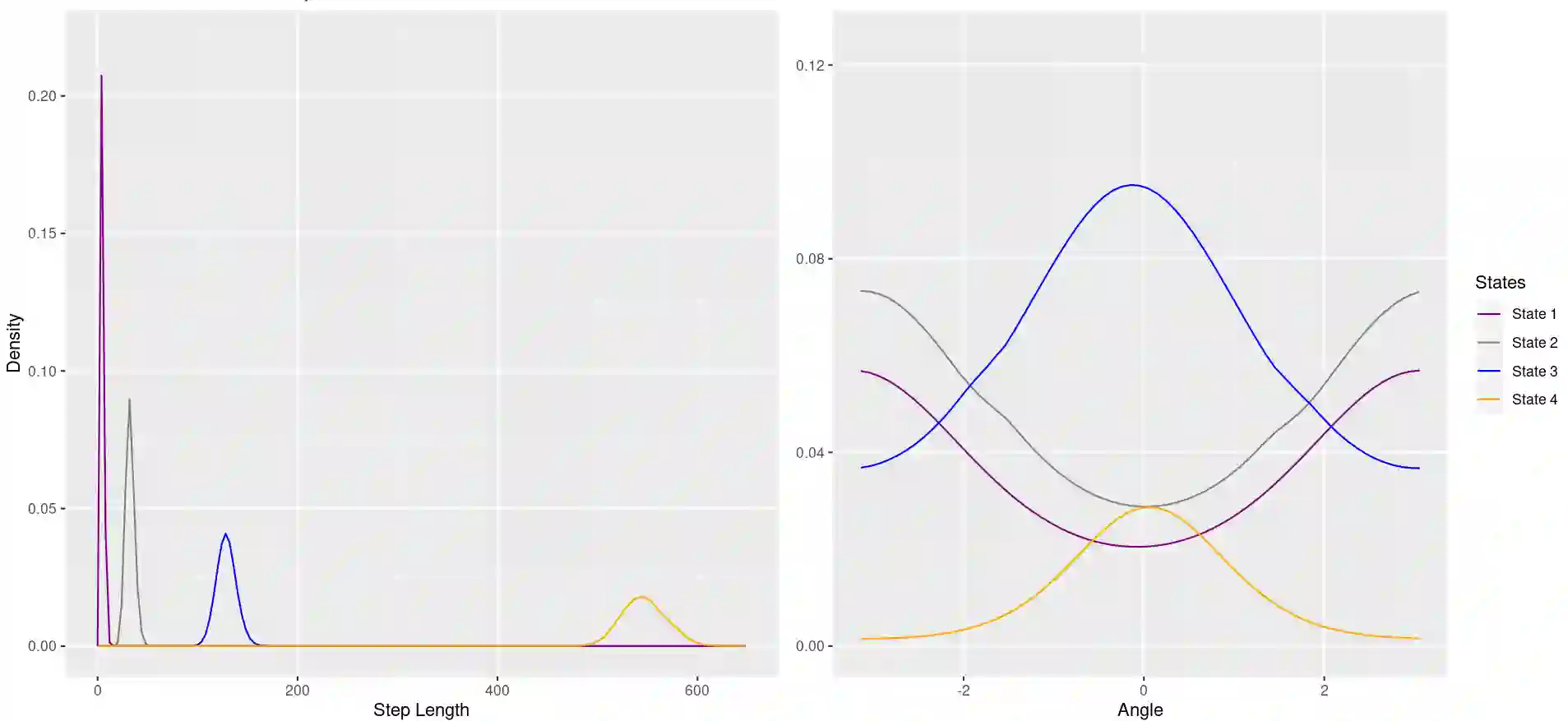
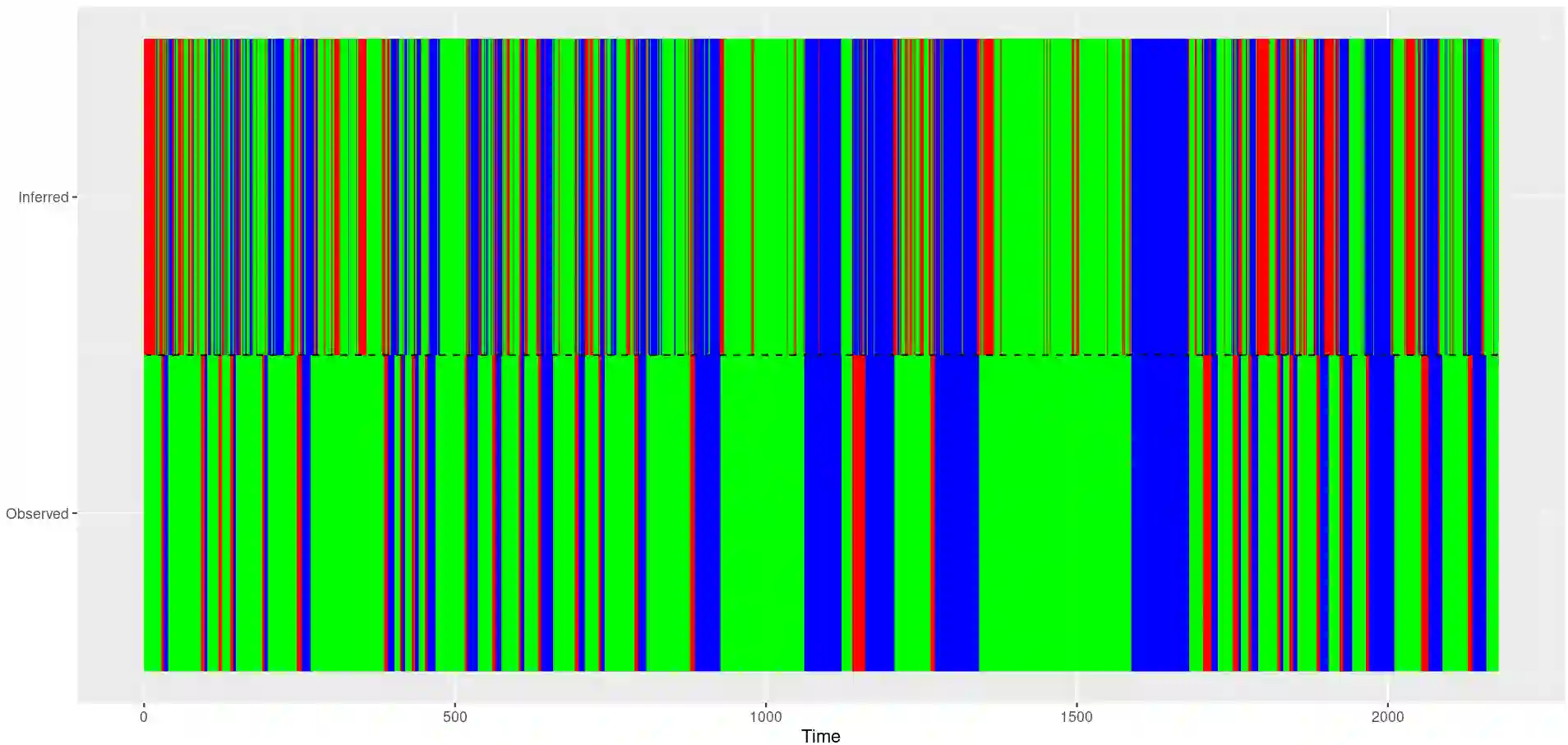
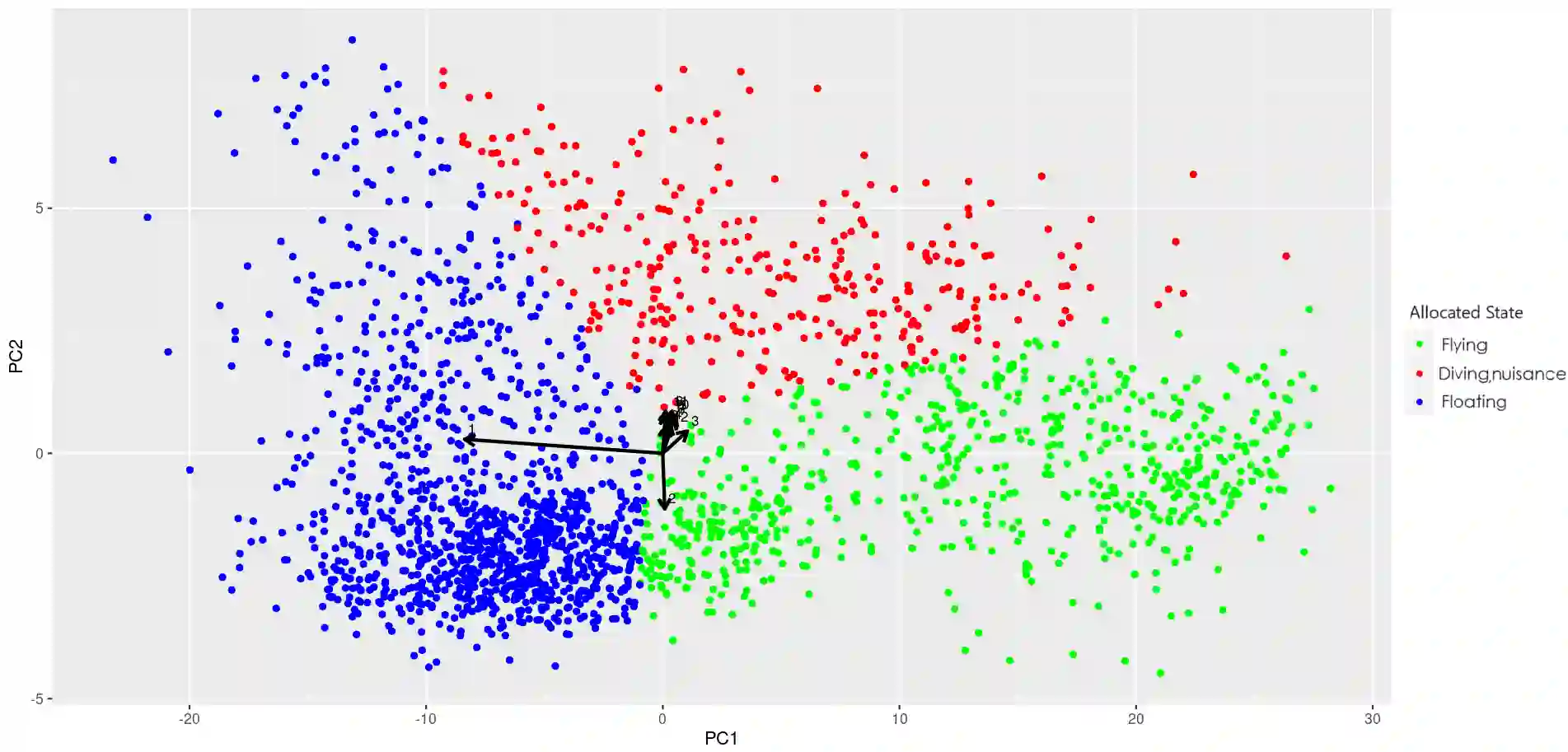
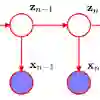
Hidden Markov models (HMMs) offer a robust and efficient framework for analyzing time series data, modelling both the underlying latent state progression over time and the observation process, conditional on the latent state. However, a critical challenge lies in determining the appropriate number of underlying states, often unknown in practice. In this paper, we employ a Bayesian framework, treating the number of states as a random variable and employing reversible jump Markov chain Monte Carlo to sample from the posterior distributions of all parameters, including the number of states. Additionally, we introduce repulsive priors for the state parameters in HMMs, and hence avoid overfitting issues and promote parsimonious models with dissimilar state components. We perform an extensive simulation study comparing performance of models with independent and repulsive prior distributions on the state parameters, and demonstrate our proposed framework on two ecological case studies: GPS tracking data on muskox in Antarctica and acoustic data on Cape gannets in South Africa. Our results highlight how our framework effectively explores the model space, defined by models with different latent state dimensions, while leading to latent states that are distinguished better and hence are more interpretable, enabling better understanding of complex dynamic systems.
翻译:暂无翻译