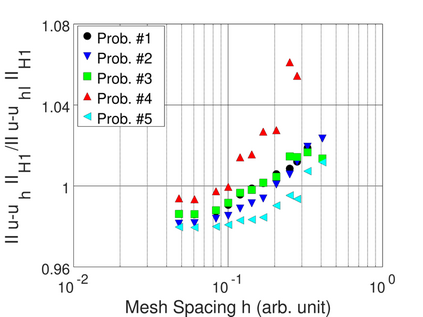
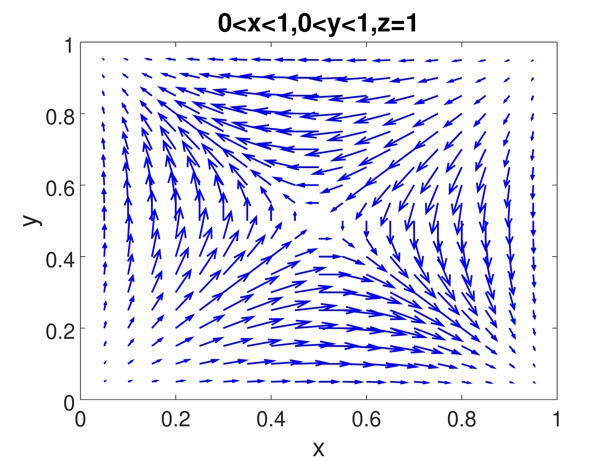
Stokes flows are a type of fluid flow where convective forces are small in comparison with viscous forces, and momentum transport is entirely due to viscous diffusion. Besides being routinely used as benchmark test cases in numerical fluid dynamics, Stokes flows are relevant in several applications in science and engineering including porous media flow, biological flows, microfluidics, microrobotics, and hydrodynamic lubrication. The present study concerns the discretization of the equations of motion of Stokes flows in three dimensions utilizing the MINI mixed finite element, focusing on the superconvergence of the method which was investigated with numerical experiments using five purpose-made benchmark test cases with analytical solution. Despite the fact that the MINI element is only linearly convergent according to standard mixed finite element theory, a recent theoretical development proves that, for structured meshes in two dimensions, the pressure superconverges with order 1.5, as well as the linear part of the computed velocity with respect to the piecewise-linear nodal interpolation of the exact velocity. The numerical experiments documented herein suggest a more general validity of the superconvergence in pressure, possibly to unstructured tetrahedral meshes and even up to quadratic convergence which was observed with one test problem, thereby indicating that there is scope to further extend the available theoretical results on convergence.
翻译:斯托克斯流流是一种流体流体,与粘结力相比,流体流体是小于一种流体的流体,动力传输完全是由于粘度扩散造成的。斯托克斯流除了经常用作数字流动态中的基准测试案例之外,在科学和工程的若干应用中也具有相关性,包括多孔的介质流、生物流、微氟化物流、微有机体流和流体动力润滑。本项研究涉及斯托克斯流运动的方程式在三个维度上离散的问题,利用MINI混合的定点元素,侧重于用5个目的设定的基准测试案例和分析性解决方案进行的数字实验所调查的方法的超级趋同性。尽管根据标准的混合定点元素理论,斯托克斯流流只是线性趋同,但最近的理论发展证明,对于结构介质为1.5的中间体,以及计算速度与精密线性节点交错的线性交错速度的线性部分,其中记录的数字实验表明,在使用5个目的基准测试案例中所调查的方法的数值试验中,其数值实验表明,根据标准的混合定点元素流体元素流体理论趋同程度,其范围范围可能延伸到一个最高压的高度,其测测测测测得的高度的高度的高度,其结果的高度范围将进一步延伸至于一个。