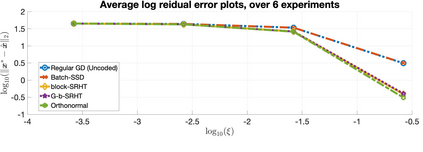
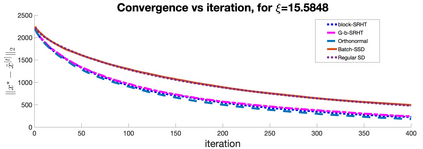
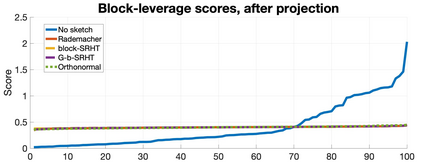
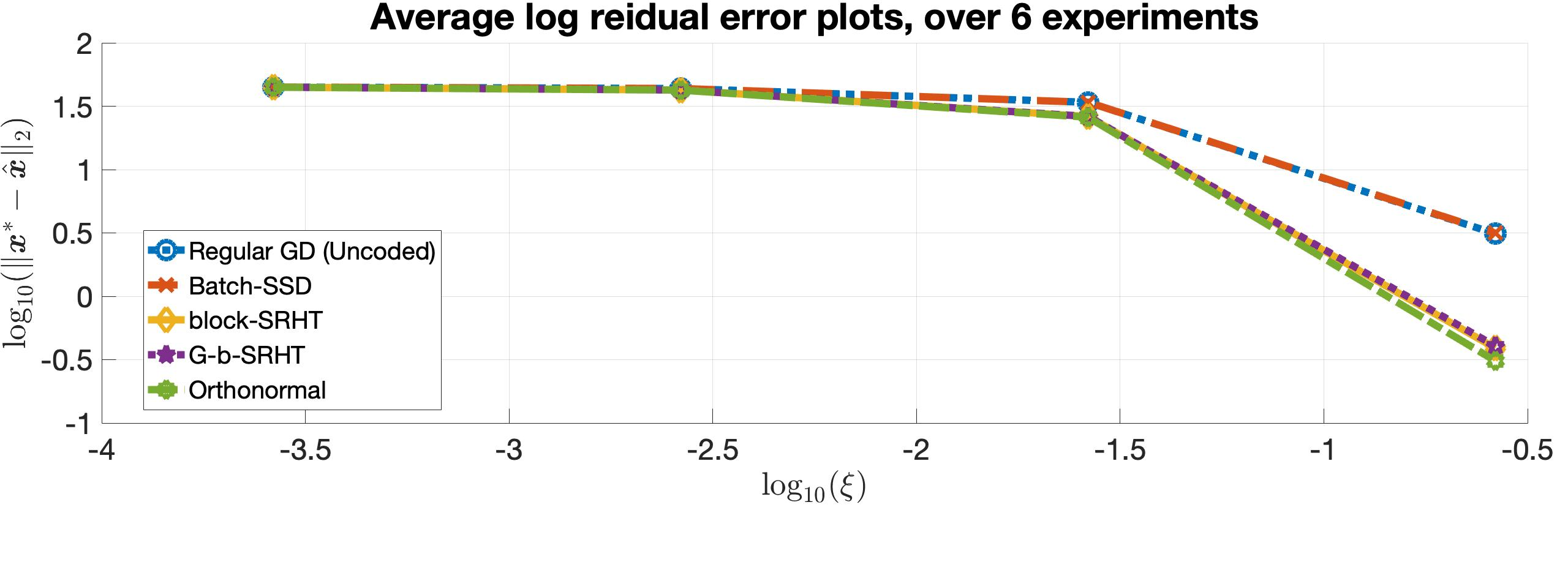
In this work, we propose a method for speeding up linear regression distributively, while ensuring security. We leverage randomized sketching techniques, and improve straggler resilience in asynchronous systems. Specifically, we apply a random orthonormal matrix and then subsample in \textit{blocks}, to simultaneously secure the information and reduce the dimension of the regression problem. In our setup, the transformation corresponds to an encoded encryption in an \textit{approximate} gradient coding scheme, and the subsampling corresponds to the responses of the non-straggling workers; in a centralized coded computing network. We focus on the special case of the \textit{Subsampled Randomized Hadamard Transform}, which we generalize to block sampling; and discuss how it can be used to secure the data. We illustrate the performance through numerical experiments.
翻译:在这项工作中,我们提出了一个在确保安全的同时加速线性回归分布的方法。 我们利用随机的草图技术, 提高非同步系统中的累进性弹性。 具体地说, 我们应用随机的正态矩阵, 然后在\ textit{ blocks} 中进行子抽样, 以同时保护信息, 并减少回归问题的维度。 在我们的设置中, 转换相当于 \ textit{ applobly} 梯度编码系统中的编码加密, 子抽样对应非分层工人的反应; 在集中的编码计算网络中。 我们集中关注 \ textit{ Subsamped Randomiced Hadamad 变形 的特例, 我们用它来封隔断取样; 并讨论如何使用它来保护数据。 我们通过数字实验来说明它的性能 。