A unified view for unsupervised representation learning with density ratio estimation: Maximization of mutual information, nonlinear ICA and nonlinear subspace estimation

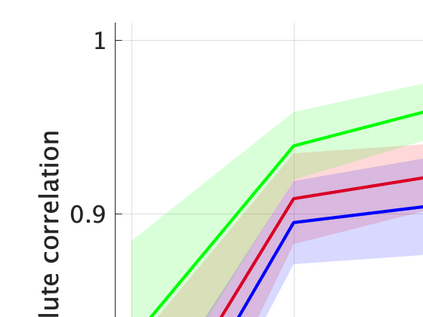
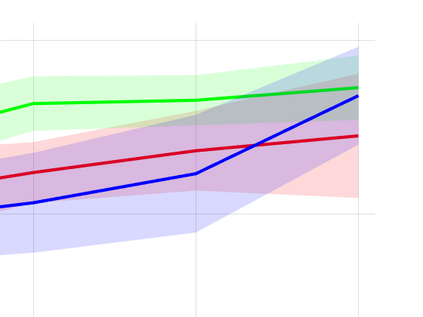
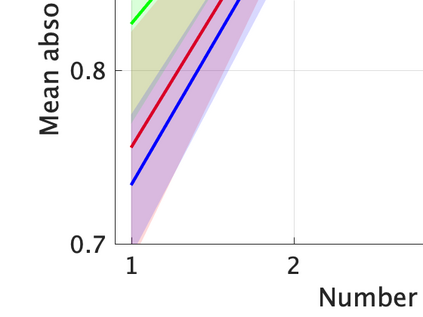
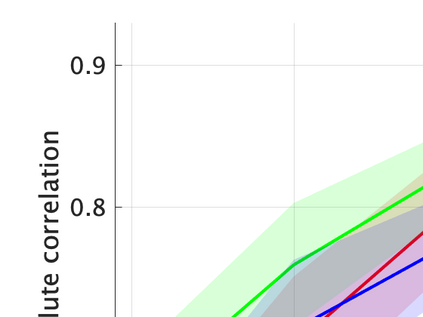
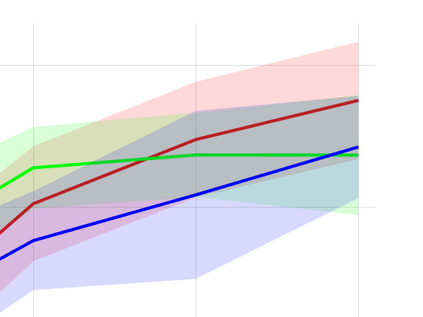
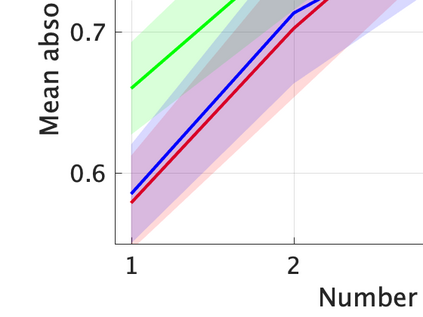
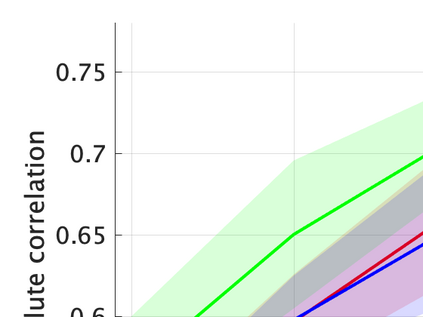
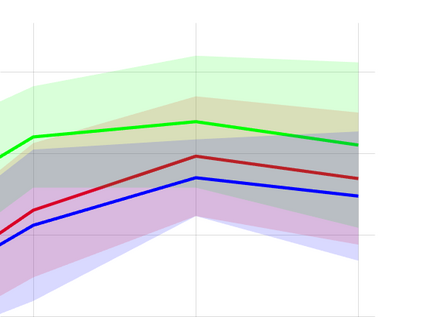
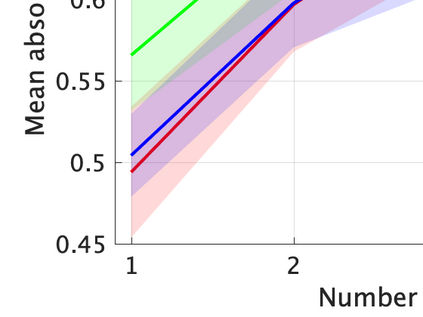
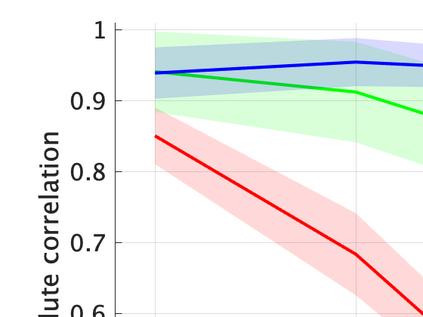
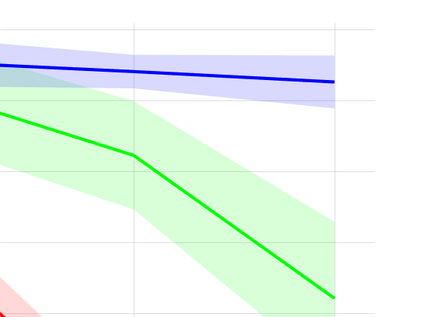
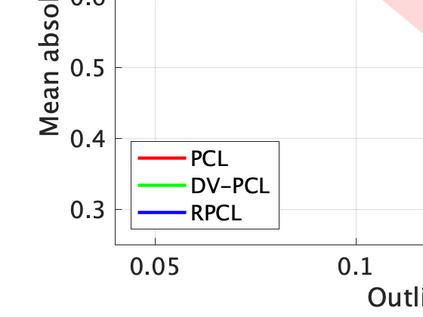
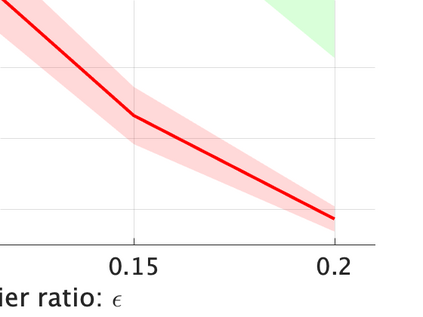
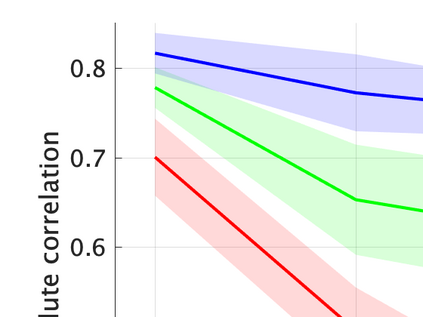
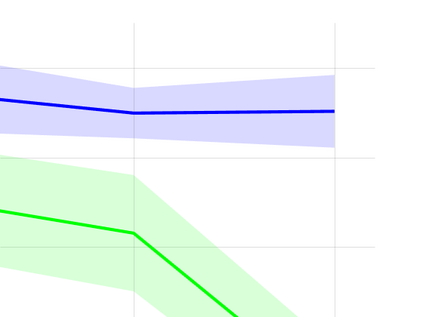
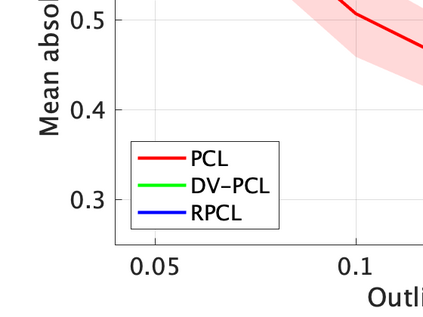
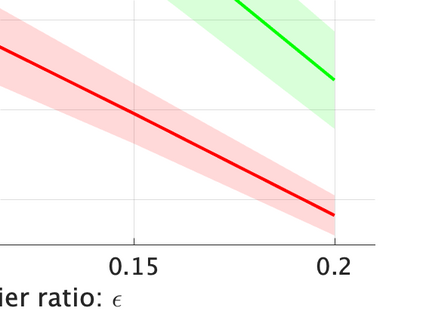
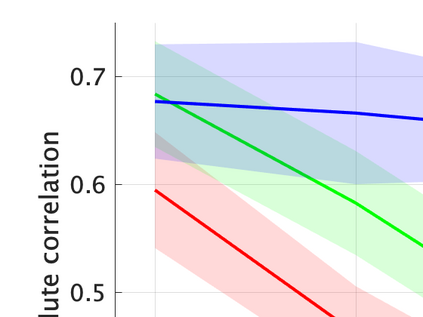
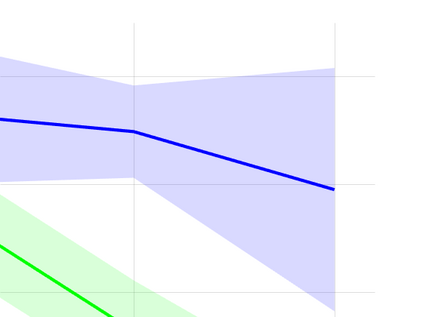
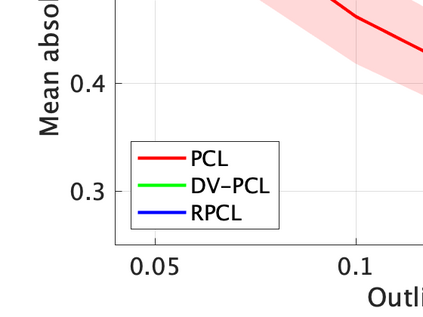
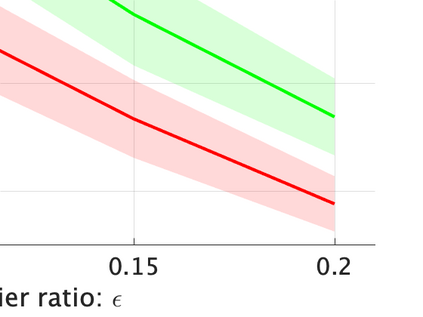
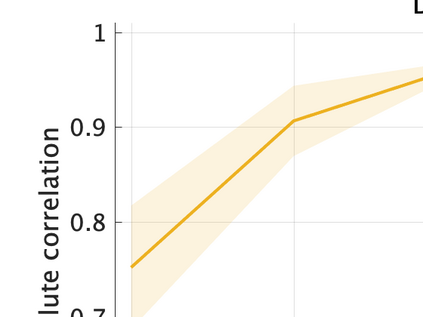
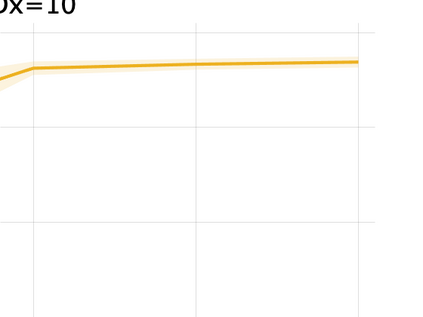
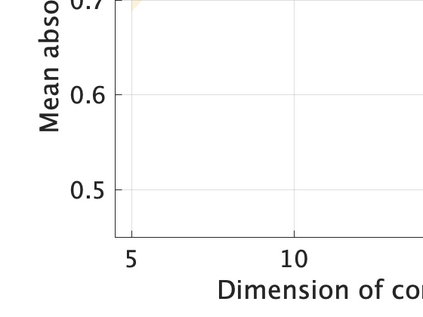
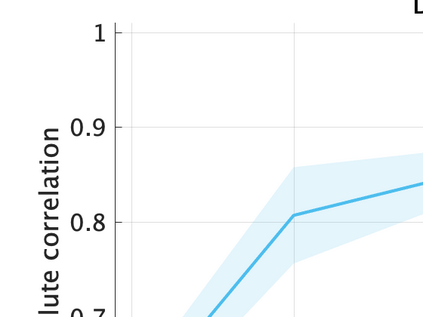
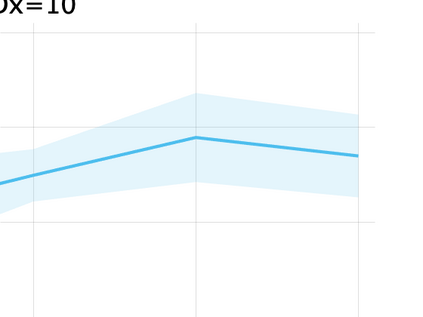
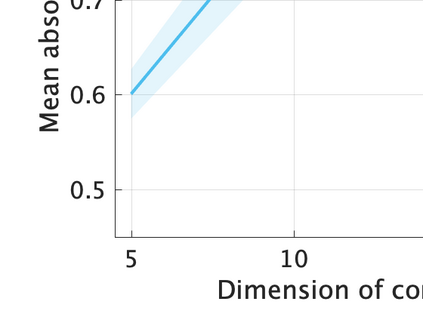
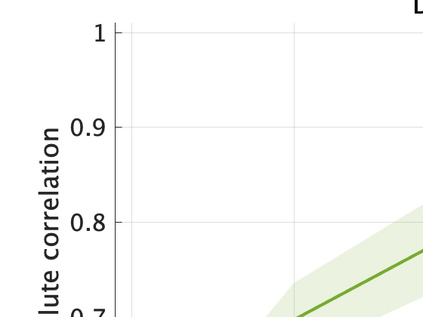
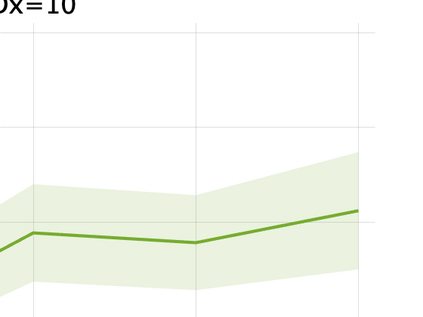
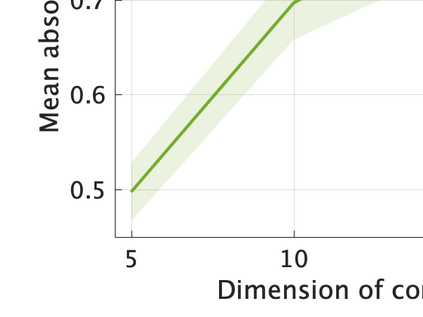
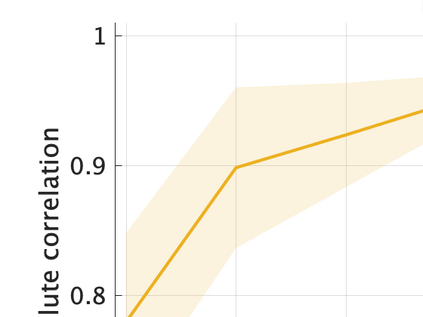
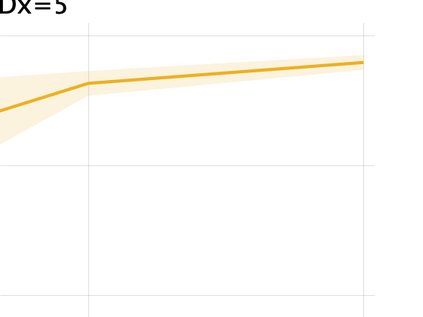
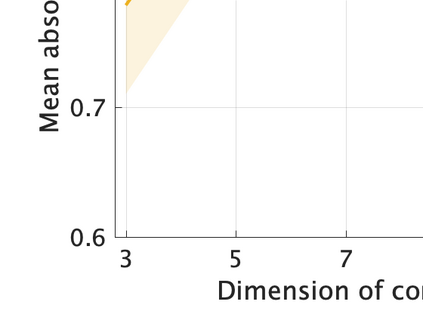
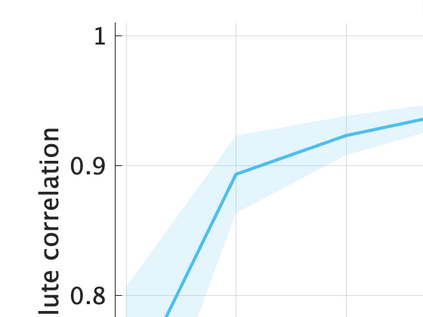
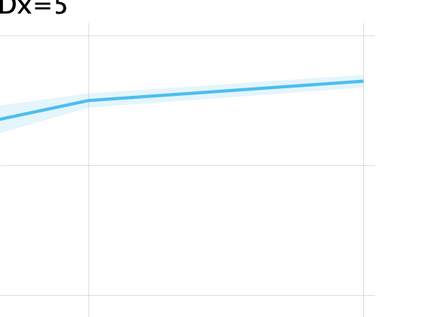
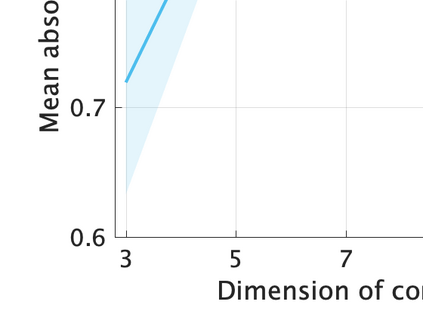
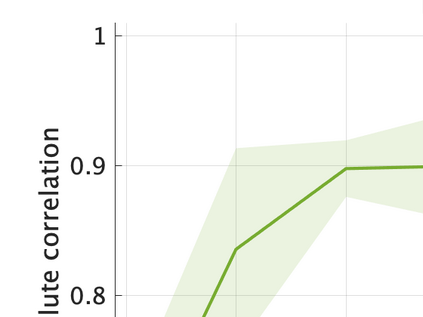
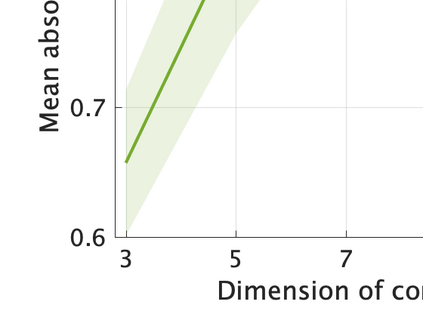
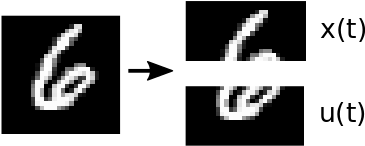
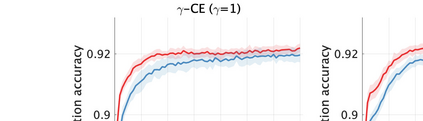
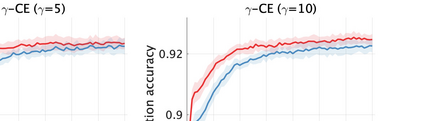
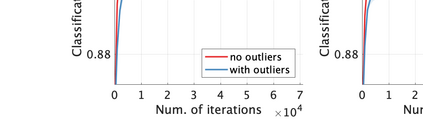
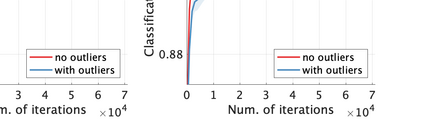
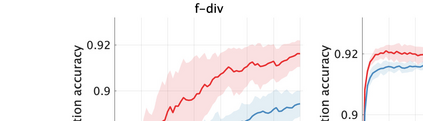
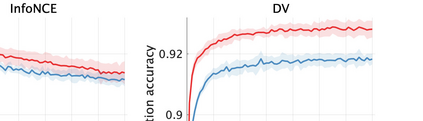
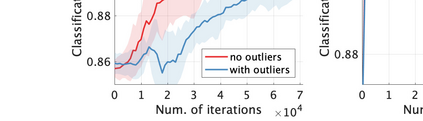
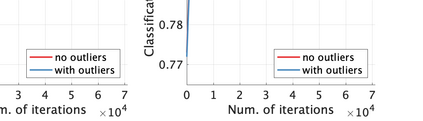
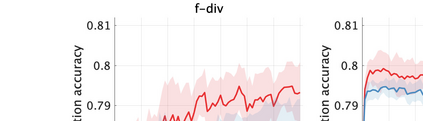
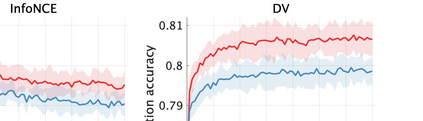
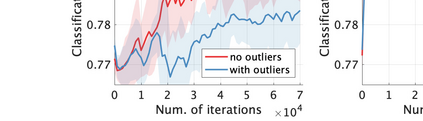
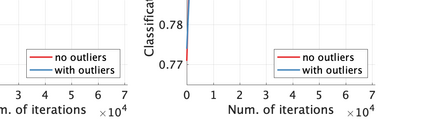
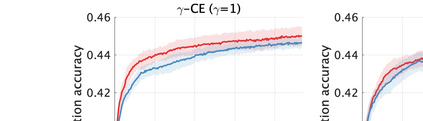
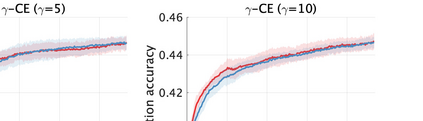
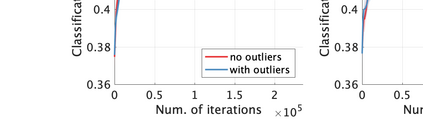
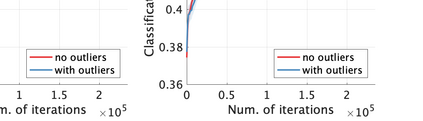
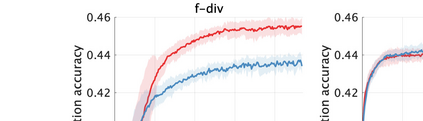
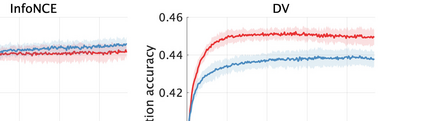
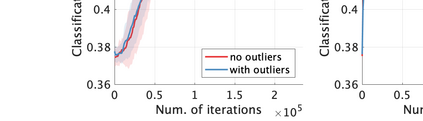
Unsupervised representation learning is one of the most important problems in machine learning. Recent promising methods are based on contrastive learning. However, contrastive learning often relies on heuristic ideas, and therefore it is not easy to understand what contrastive learning is doing. This paper emphasizes that density ratio estimation is a promising goal for unsupervised representation learning, and promotes understanding to contrastive learning. Our primal contribution is to theoretically show that density ratio estimation unifies three frameworks for unsupervised representation learning: Maximization of mutual information (MI), nonlinear independent component analysis (ICA) and a novel framework for estimation of a lower-dimensional nonlinear subspace proposed in this paper. This unified view clarifies under what conditions contrastive learning can be regarded as maximizing MI, performing nonlinear ICA or estimating the lower-dimensional nonlinear subspace in the proposed framework. Furthermore, we also make theoretical contributions in each of the three frameworks: We show that MI can be maximized through density ratio estimation under certain conditions, while our analysis for nonlinear ICA reveals a novel insight for recovery of the latent source components, which is clearly supported by numerical experiments. In addition, some theoretical conditions are also established to estimate a nonlinear subspace in the proposed framework. Based on the unified view, we propose two practical methods for unsupervised representation learning through density ratio estimation: The first method is an outlier-robust method for representation learning, while the second one is a sample-efficient nonlinear ICA method. Finally, we numerically demonstrate usefulness of the proposed methods in nonlinear ICA and through application to a downstream task for classification.