Combining resampling and reweighting for faithful stochastic optimization

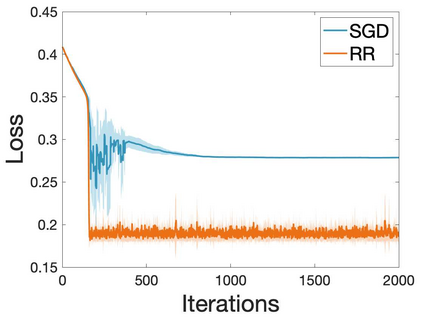
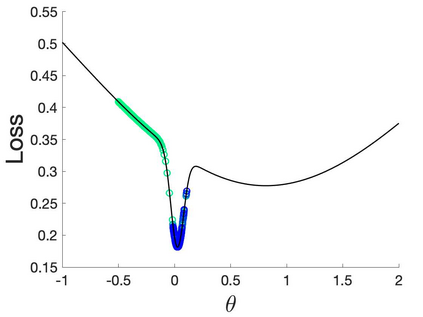
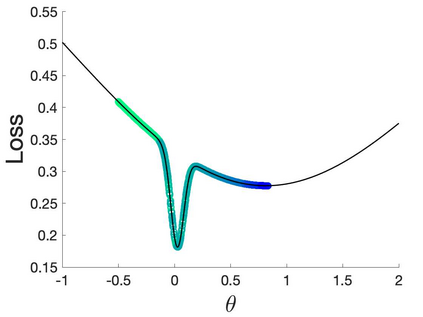
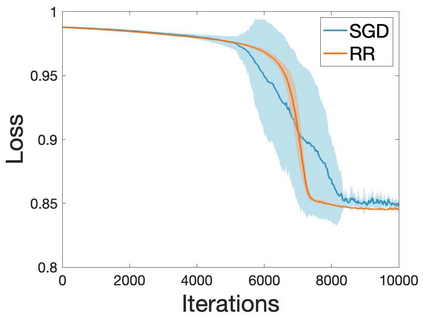
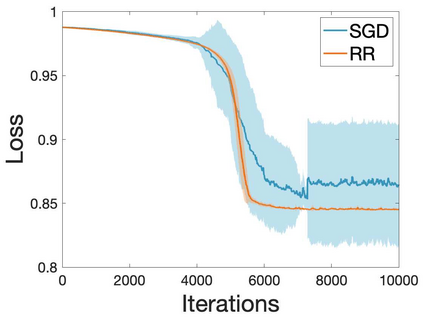
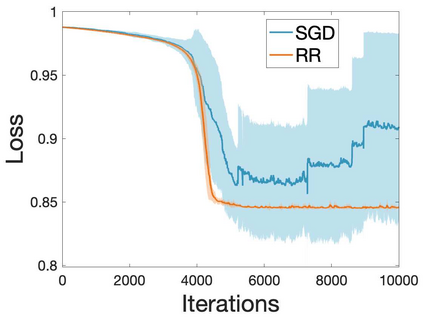
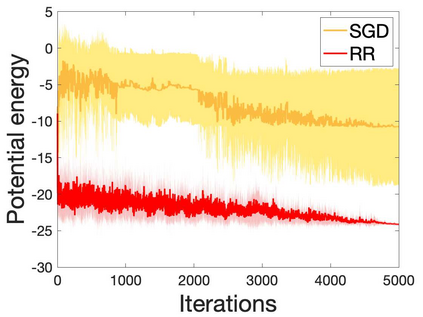
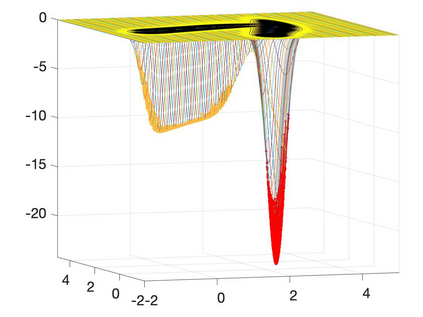
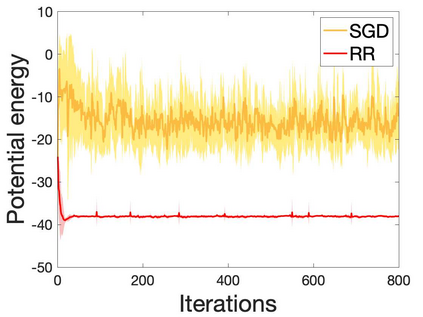
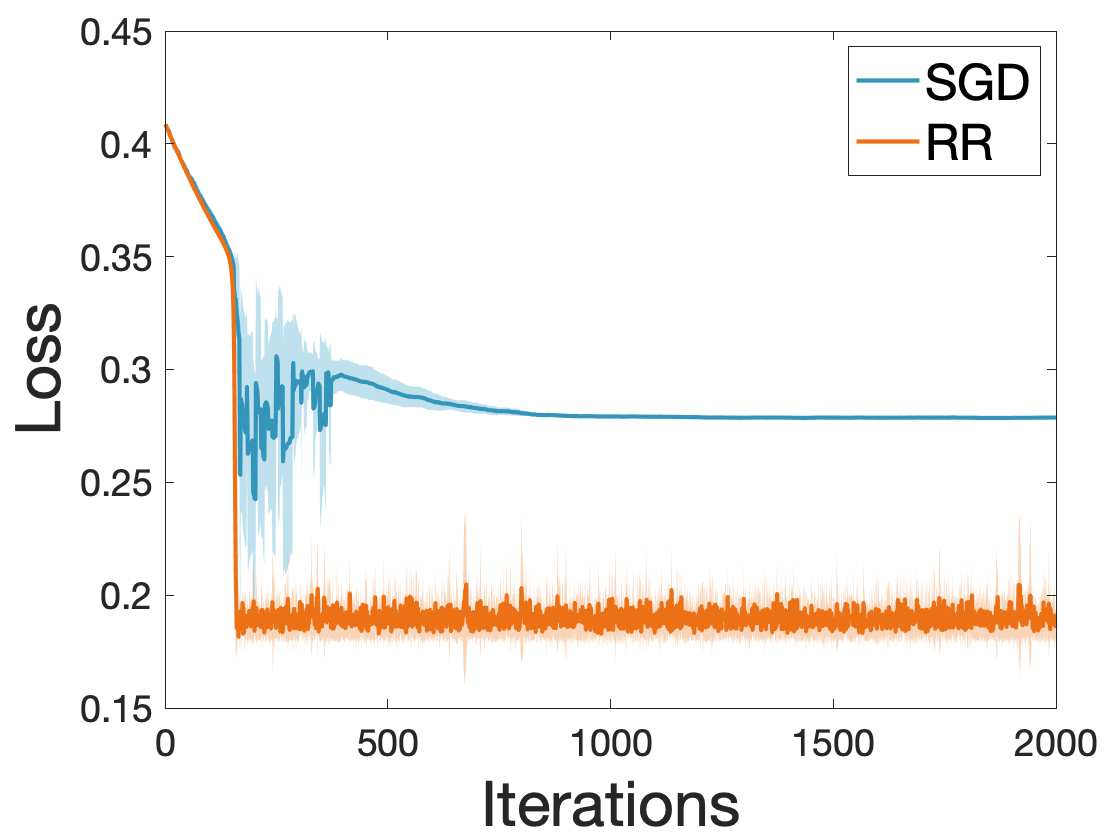
Many machine learning and data science tasks require solving non-convex optimization problems. When the loss function is a sum of multiple terms, a popular method is the stochastic gradient descent. Viewed as a process for sampling the loss function landscape, the stochastic gradient descent is known to prefer flat minima. Though this is desired for certain optimization problems such as in deep learning, it causes issues when the goal is to find the global minimum, especially if the global minimum resides in a sharp valley. Illustrated with a simple motivating example, we show that the fundamental reason is that the difference in the Lipschitz constants of multiple terms in the loss function causes stochastic gradient descent to experience different variances at different minima. In order to mitigate this effect and perform faithful optimization, we propose a combined resampling-reweighting scheme to balance the variance at local minima and extend to general loss functions. We explain from the numerical stability perspective how the proposed scheme is more likely to select the true global minimum, and the local convergence analysis perspective how it converges to a minimum faster when compared with the vanilla stochastic gradient descent. Experiments from robust statistics and computational chemistry are provided to demonstrate the theoretical findings.