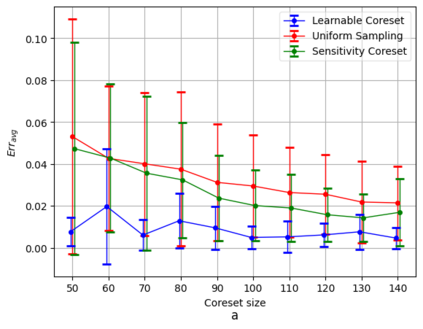
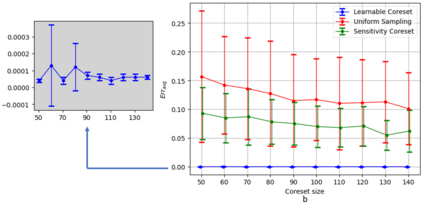
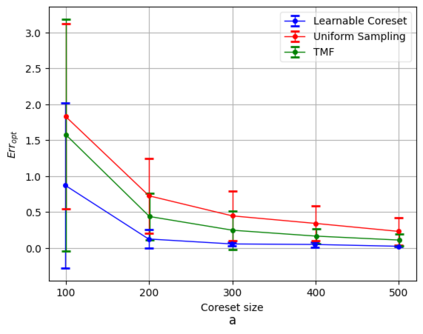
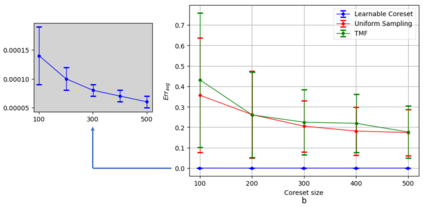
Coreset of a given dataset and loss function is usually a small weighed set that approximates this loss for every query from a given set of queries. Coresets have shown to be very useful in many applications. However, coresets construction is done in a problem dependent manner and it could take years to design and prove the correctness of a coreset for a specific family of queries. This could limit coresets use in practical applications. Moreover, small coresets provably do not exist for many problems. To address these limitations, we propose a generic, learning-based algorithm for construction of coresets. Our approach offers a new definition of coreset, which is a natural relaxation of the standard definition and aims at approximating the \emph{average} loss of the original data over the queries. This allows us to use a learning paradigm to compute a small coreset of a given set of inputs with respect to a given loss function using a training set of queries. We derive formal guarantees for the proposed approach. Experimental evaluation on deep networks and classic machine learning problems show that our learned coresets yield comparable or even better results than the existing algorithms with worst-case theoretical guarantees (that may be too pessimistic in practice). Furthermore, our approach applied to deep network pruning provides the first coreset for a full deep network, i.e., compresses all the network at once, and not layer by layer or similar divide-and-conquer methods.
翻译:给定的数据集和损失函数的核心集通常是一个小的称重的集合, 与给定的一组查询的每个查询的这一损失相近。 核心集显示在许多应用中非常有用。 但是, 核心集的构造是以一种取决于问题的方式完成的, 可能要花几年时间来设计和证明特定查询组核心集的正确性。 这可能会限制在实际应用中使用的核心集。 此外, 小核心集对于许多问题并不存在。 为了解决这些局限性, 我们为构建核心集提出了一种通用的、 学习性的算法。 我们的方法为构建核心集提供了一个新的定义。 我们的方法提供了一种对核心集的新定义, 这是对标准定义的自然放松, 目的是在查询的原始数据中接近 emph{ 平均 。 这使我们能够用学习的范式来对特定损失函数的一组小核心集进行拼凑。 我们为拟议的方法提供了正式的保证。 对深层次网络和经典机器学习问题的实验性评估表明, 我们所学过的核心小组集在深度网络中产生可比较的或更好的结果。 最深层次的计算方法可能由最坏的理论级的网络提供最深层次的保证, 。