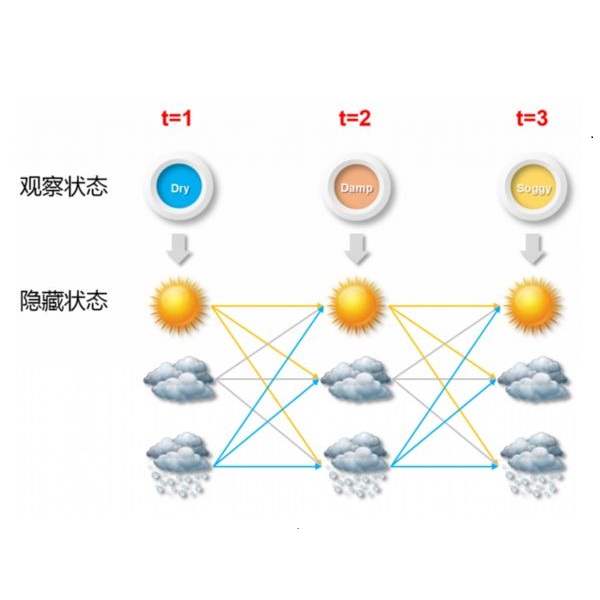
We consider the problem of estimation in Hidden Markov models with finite state space and nonparametric emission distributions. Efficient estimators for the transition matrix are exhibited, and a semiparametric Bernstein-von Mises result is deduced, extending the work of Gassiat et al. (2018) on mixture models to the HMM setting. Following from this, we propose a modular approach using the cut posterior to jointly estimate the transition matrix and the emission densities. We derive a general theorem on contraction rates for this approach, in the spirit of the seminal work of Ghosal and van der Vaart (2007). We then show how this result may be applied to obtain a contraction rate result for the emission densities in our setting; a key intermediate step is an inversion inequality relating $L^1$ distance between the marginal densities to $L^1$ distance between the emissions. Finally, a contraction result for the smoothing probabilities is shown, which avoids the common approach of sample splitting. Simulations are provided which demonstrate both the theory and the ease of its implementation.
翻译:我们考虑的是具有有限状态空间和非参数排放分布的隐性Markov模型的估计问题。展示了过渡矩阵的有效估计器,并推断出伯恩斯坦-冯·米泽斯的半参数结果,将Gassiat等人(2018年)关于混合模型的工作扩大到HMM设置。之后,我们提议采用模块化方法,使用剪切后背体联合估计过渡矩阵和排放密度。我们本着Ghosal和van der Vaart(2007年)的开创性工作精神,得出了这一方法的收缩率的一般理论。然后,我们展示了如何应用这一结果来获取我们设置的排放密度收缩率结果;一个关键的中间步骤是将边际密度之间的距离拉1美元至排放之间的距离拉1美元。最后,显示了平滑概率的收缩结果,从而避免了样本分离的共同方法。提供了既能说明理论又能便于执行的模拟。