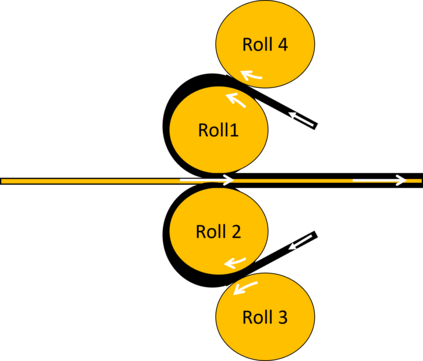
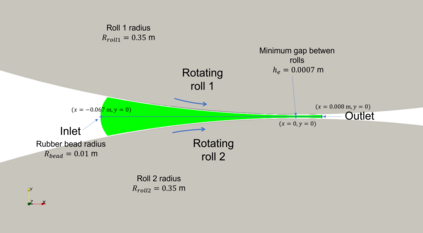
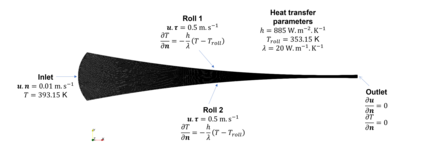
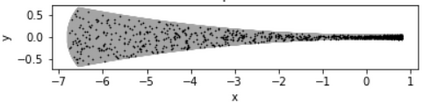
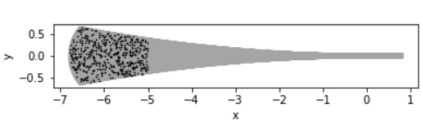
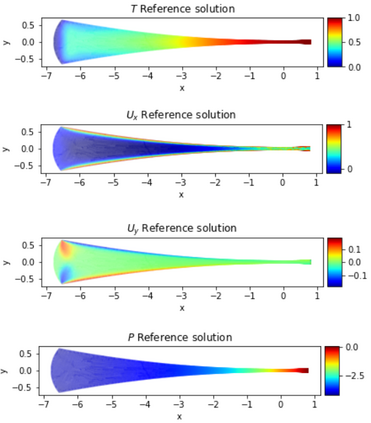
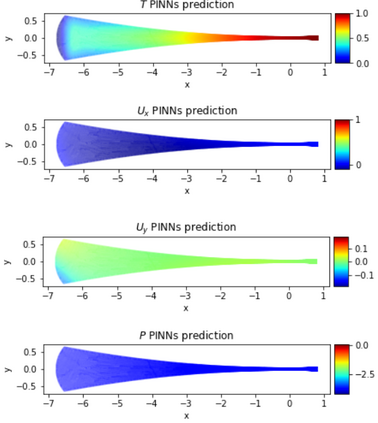
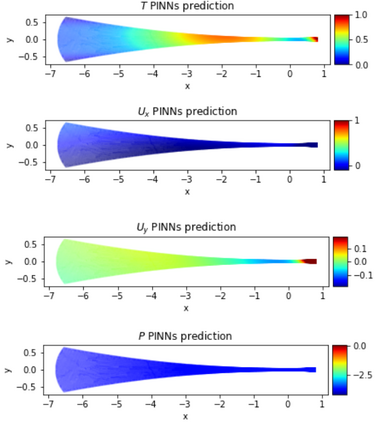
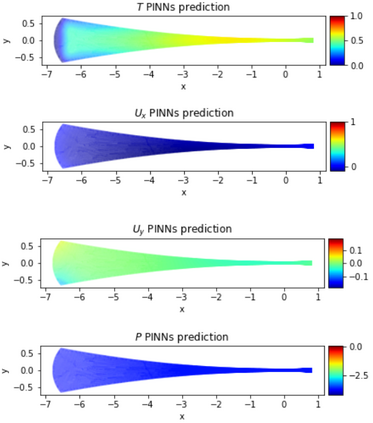
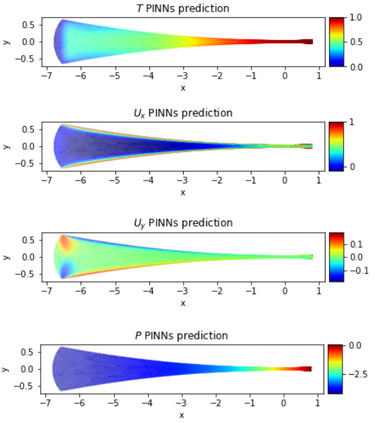
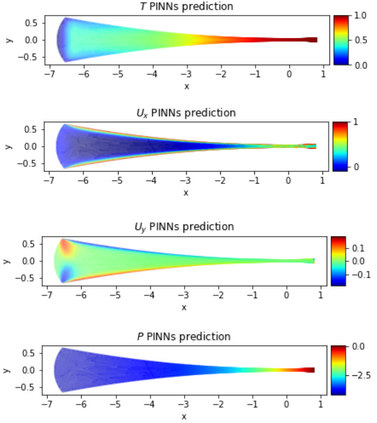
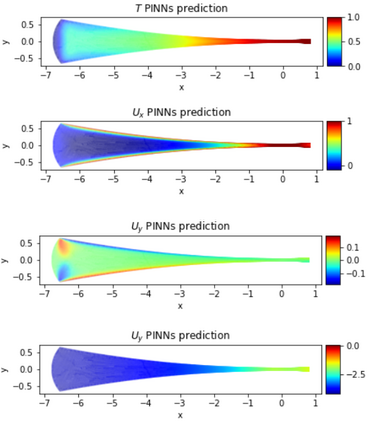
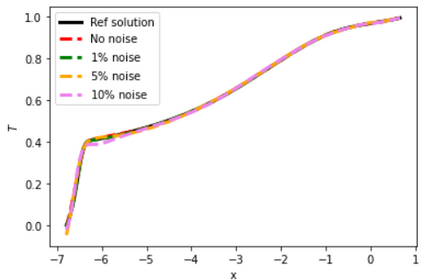
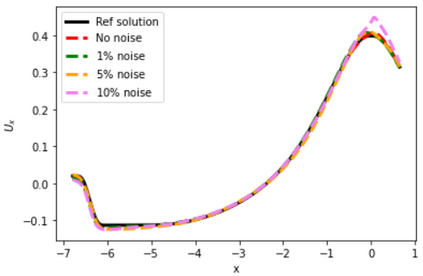
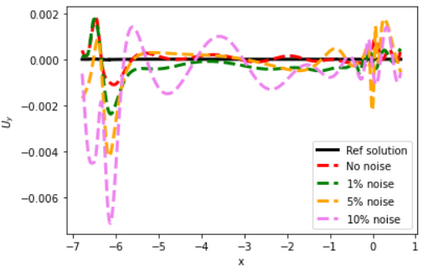
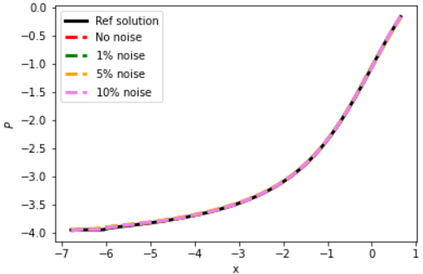
Physics-Informed Neural Networks (PINNs) have gained much attention in various fields of engineering thanks to their capability of incorporating physical laws into the models. However, the assessment of PINNs in industrial applications involving coupling between mechanical and thermal fields is still an active research topic. In this work, we present an application of PINNs to a non-Newtonian fluid thermo-mechanical problem which is often considered in the rubber calendering process. We demonstrate the effectiveness of PINNs when dealing with inverse and ill-posed problems, which are impractical to be solved by classical numerical discretization methods. We study the impact of the placement of the sensors and the distribution of unsupervised points on the performance of PINNs in a problem of inferring hidden physical fields from some partial data. We also investigate the capability of PINNs to identify unknown physical parameters from the measurements captured by sensors. The effect of noisy measurements is also considered throughout this work. The results of this paper demonstrate that in the problem of identification, PINNs can successfully estimate the unknown parameters using only the measurements on the sensors. In ill-posed problems where boundary conditions are not completely defined, even though the placement of the sensors and the distribution of unsupervised points have a great impact on PINNs performance, we show that the algorithm is able to infer the hidden physics from local measurements.
翻译:由于能够将物理法将物理法纳入模型,物理进化神经网络(PINNs)在各个工程领域引起了许多注意。然而,在机械和热场之间结合的工业应用中,对PINNs在工业应用中的PINNs的评估仍是一个积极的研究课题。在这项工作中,我们将PINNs应用于一个非牛顿流体热机械化问题,这个问题经常在橡胶计算过程中得到考虑。我们显示了PINNs在处理反向和错误的问题时的有效性,这些问题不可能通过传统的数字分解方法解决。我们研究了在机械和热场之间结合的工业应用中安装传感器和分配未受监督的点对PINNs性能的影响。我们还调查PINNs在从传感器采集的测量中找出未知的物理参数的能力。在整个工作中也考虑到噪音测量的影响。本文的结果表明,在识别问题时,PINNs的条件甚至能够用传统的数字分解方法来评估未知参数。我们只能用传感器的测量结果来评估PINNsnvisat 点对PINs的性能彻底的测算结果。我们所定义的精确测测测测测测测到的测测测测测到的传感器的测测测测到的测到的测测测到的测测点的测点。我们测测到的测测测到的测测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的测到的深度的问题。