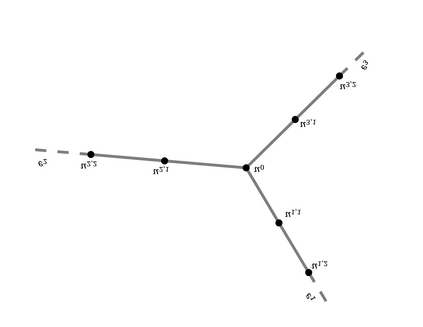
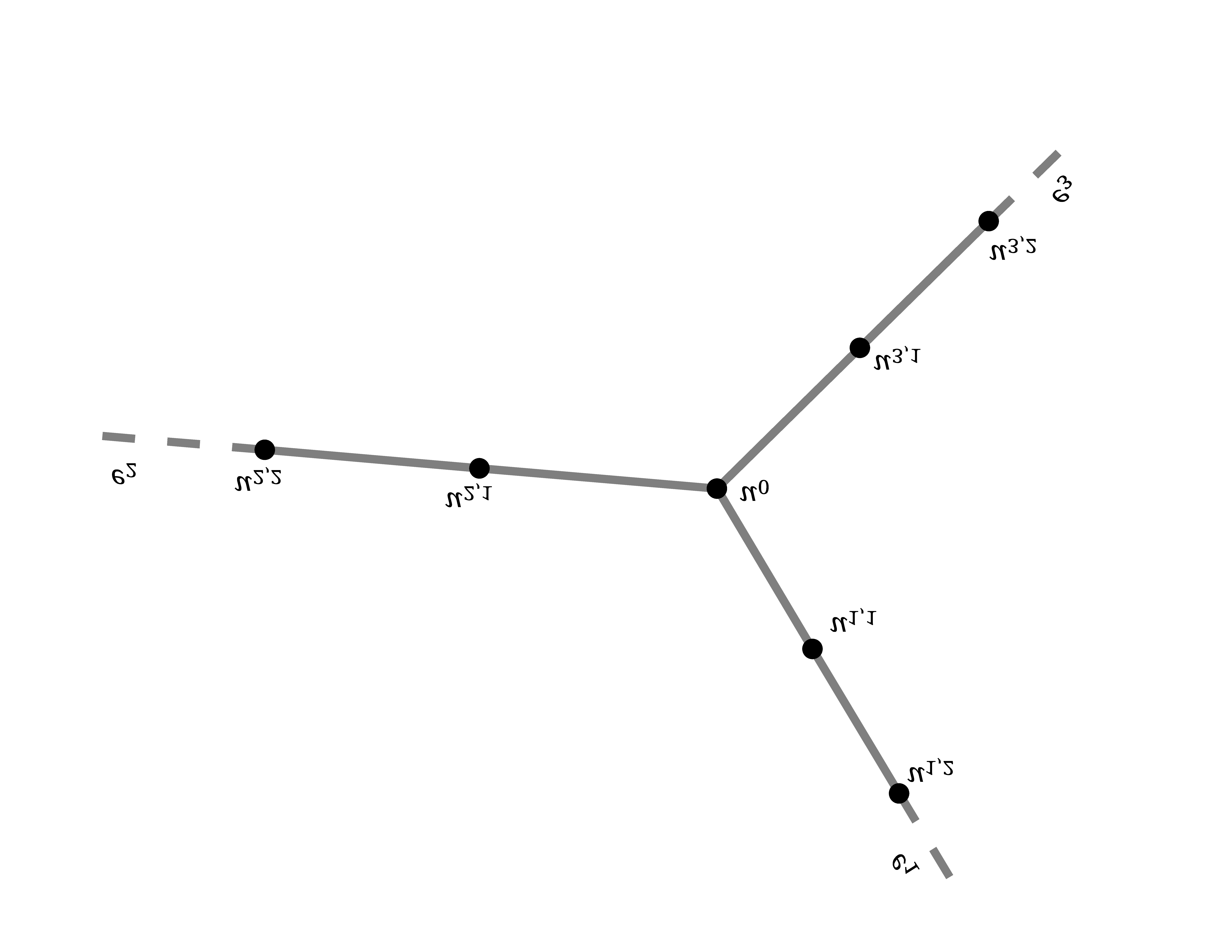
To solve linear PDEs on metric graphs with standard coupling conditions (continuity and Kirchhoff's law), we develop and compare a spectral, a second-order finite difference, and a discontinuous Galerkin method. The spectral method yields eigenvalues and eigenvectors of arbitary order with machine precision and converges exponentially. These eigenvectors provide a Fourier-like basis on which to expand the solution; however, more complex coupling conditions require additional research. The discontinuous Galerkin method provides approximations of arbitrary polynomial order; however computing high-order eigenvalues accurately requires the respective eigenvector to be well-resolved. The method allows arbitrary non-Kirchhoff flux conditions and requires special penalty terms at the vertices to enforce continuity of the solutions. For the finite difference method, the standard one-sided second-order finite difference stencil reduces the accuracy of the vertex solution to $ O(h^{3/2})$. To preserve overall second-order accuracy, we used ghost cells for each edge. For all three methods we provide the implementation details, their validation, and examples illustrating their performance for the eigenproblem, Poisson equation, and the wave equation.
翻译:为了用标准组合条件(连续和Kirchhoff法)解决图中线性PDE,我们开发并比较光谱、二级定值差异和不连续的Galerkin方法。光谱方法产生机器精度和指数趋同的任意非基质值和自然秩序的精度值和源源数。这些源源量为扩大解决方案提供了类似Fourier的基础;然而,更复杂的组合条件需要额外的研究。不连续的Galerkin方法提供了任意的多元顺序的近似值;然而,高序电子值的精确度要求相关电子元源量的完全解析。该方法允许任意的非基质值通量条件,并要求在脊椎处有特殊的惩罚条件,以强制解决方案的连续性。对于有限的差异方法,标准一至二级定值差异的Stencil降低了逆差的精确度为 $ O ( ⁇ 3/2} 。为了保存总体的二次序列精度,我们使用的幽等式模型,我们为每个边端的等式模型。