Analysis of an interventional protein experiment using a vine copula based structural equation model

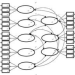
While there is considerable effort to identify signaling pathways using linear Gaussian Bayesian networks from data, there is less emphasis of understanding and quantifying conditional densities and probabilities of nodes given its parents from the identifed Bayesian network. Most graphical models for continuous data assume a multivariate Gaussian distribution, which might be too restrictive. We re-analyse data from an experimental setting considered in Sachs et al. (2005) to illustrate the effects of such restrictions. For this we propose a novel non Gaussian nonlinear structural equation model based on vine copulas. In particular the D-vine regression approach of Kraus and Czado (2017) is adapted. We show that this model class is more suited to fit the data than the standard linear structural equation model based on the biological consent graph given in Sachs et al. (2005). The modelling approach also allows to study which pathway edges are supported by the data and which can be removed. For data experiment cd3cd28+aktinhib this approach identified three edges, which are no longer supported by the data. For each of these edges a plausible explanation based on underlying the experimental conditions could be found.