Distance covariance for random fields

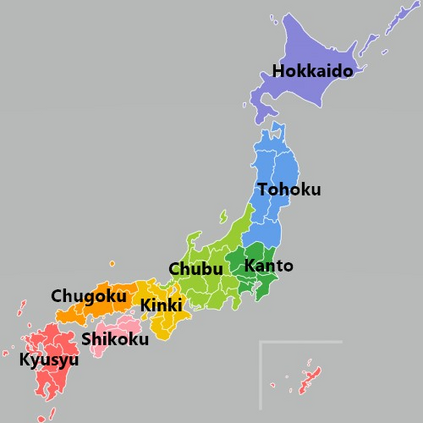
We study an independence test based on distance correlation for random fields $(X,Y)$. We consider the situations when $(X,Y)$ is observed on a lattice with equidistant grid sizes and when $(X,Y)$ is observed at random locations. We provide \asy\ theory for the sample distance correlation in both situations and show bootstrap consistency. The latter fact allows one to build a test for independence of $X$ and $Y$ based on the considered discretizations of these fields. We illustrate the performance of the bootstrap test in a simulation study involving fractional Brownian and infinite variance stable fields. The independence test is applied to Japanese meteorological data, which are observed over the entire area of Japan.