基于压缩感知的稀疏信号重建算法的理论研究

项目名称： 基于压缩感知的稀疏信号重建算法的理论研究

项目编号： No.11201450

项目类型： 青年科学基金项目

立项/批准年度： 2013

项目学科： 数理科学和化学

项目作者： 黄尉

作者单位： 中国科学技术大学

项目金额： 22万元

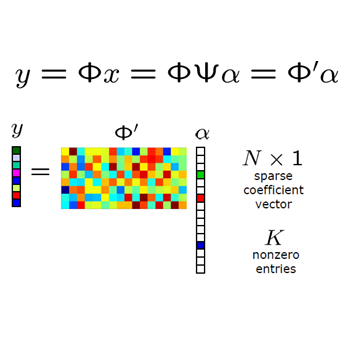
中文摘要： 压缩感知理论是近几年信号处理领域兴起的前沿课题。与传统采样不同，压缩采样把信号压缩融合到采样中，其采样频率可远低丁奈奎斯特频率，有效降低了信息传输、存贮的数据量。压缩感知的一个重要任务就是对压缩采样后的信号进行重构，目前引起了众多学者的关注和研究。 本项目的主要目标是，结合学习理论中的稀疏正则化算法，针对实际问题中一类特殊结构的信号- - 块稀疏信号的特点, 提出若干种快速重构算法，研究算法的收敛性，并探讨算法的理论基础；同时开展基于冗余字典的稀疏信号恢复算法研究以及探讨压缩感知和最佳K项逼近的内在联系。本项目属于压缩感知中重构算法的理论及应用研究， 具有一定的理论价值和广泛的应用前景。

中文关键词： 压缩感知；稀疏正则化；限制等距性质；稀疏恢复；非凸优化

英文摘要： Compressed Sensing (CS) is an emerging area in signal processing domain these years. Compared with traditional sampling, CS integrates compression into the sampling process, which significantly reduces the data for transmission and storage. One of the important tasks in CS is how to recover the signals more accurately and effectively, which is concerned by many researchers. Focus on the practical problems that the special structure of the signals-block sparse signals, the major goal of this project is present some fast algorithms which are combined with the sparse regularization algorithm in learning theory. We discuss the theoretical foundation of these algorithms, the convergence criteria is also given. Simultaneously, we consider sparse recovery algorithm via overcomplete dictionaries , the inherent relations between compressed sensing and best k-term approximation is also discussed. This project belongs to the theory and application of reconstruction algorithms in compressed sensing. The study is of important theoretical value and practical significance.

英文关键词： Compressed sensing；sparse regularization；restricted isometry property；sparse recovery；non-convex optimization