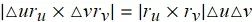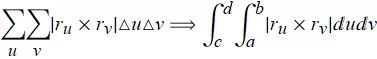【参数化曲面】图解高等数学-下 26
13.6 参数化曲面
显示: z = f(x,y)
隐式: F(x,y,z) = 0
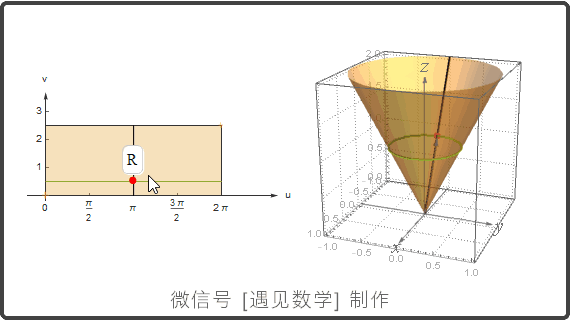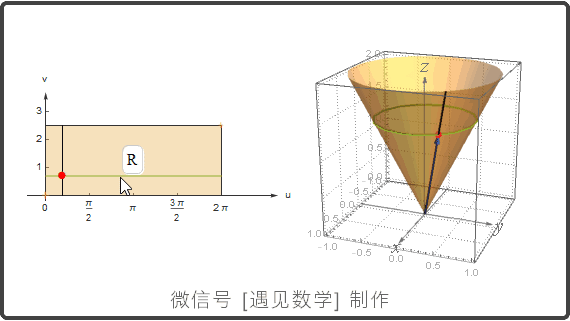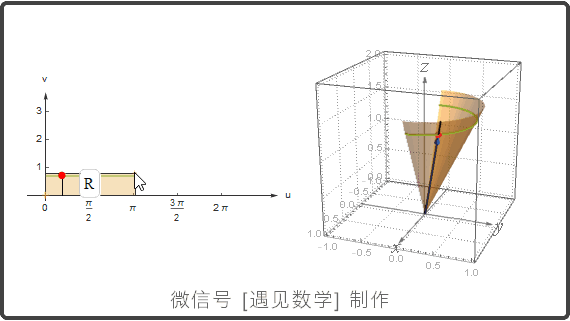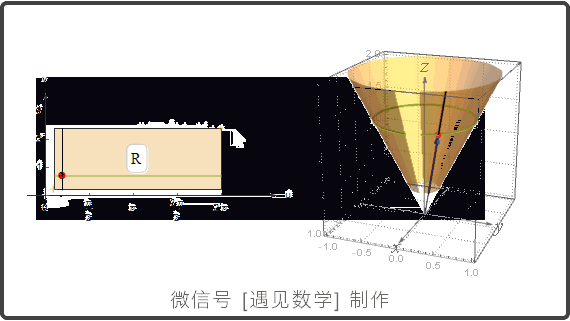
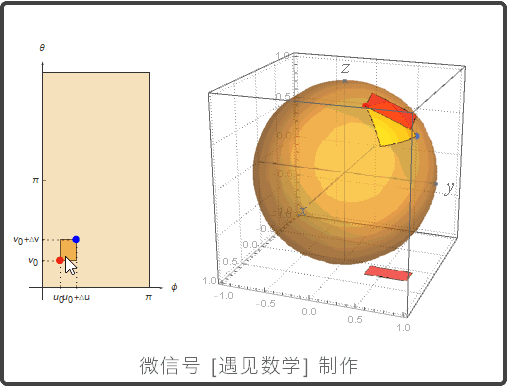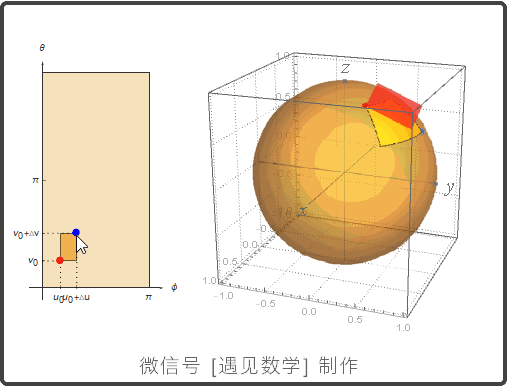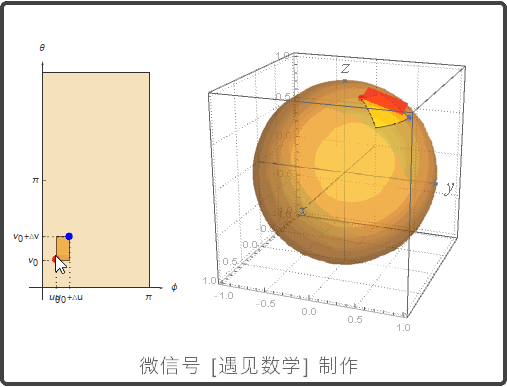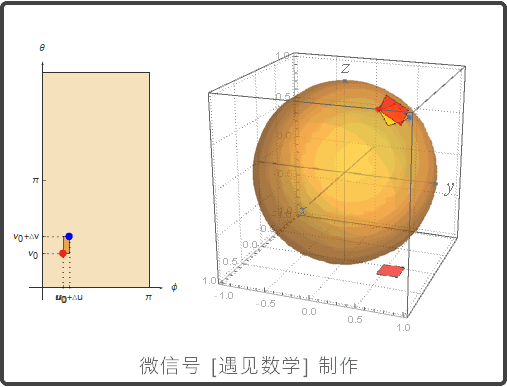
参数化曲面: r(u,v) = f(u,v)i + g(u,v)j + h(u,v)k
曲面参数化
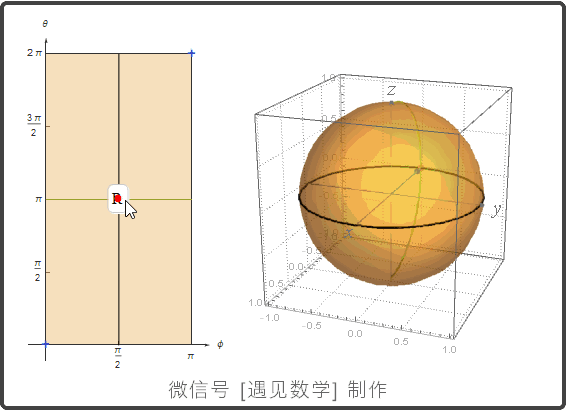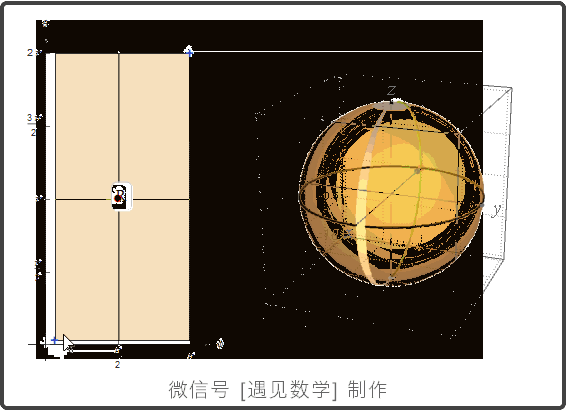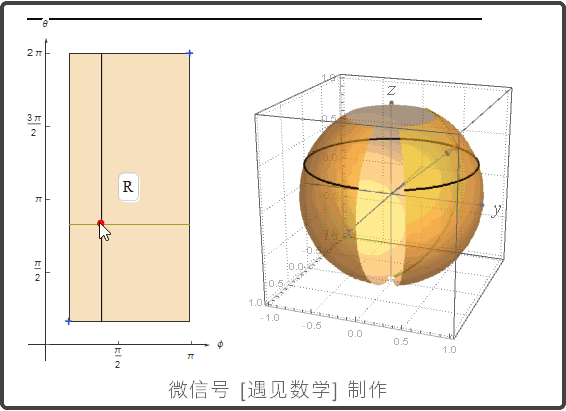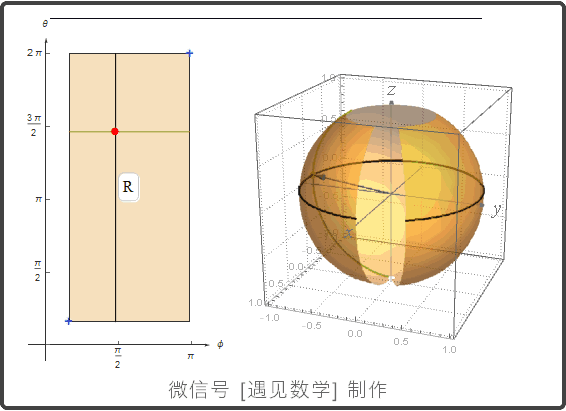
球面的参数化
曲面面积
曲面积分
遇见数学, 遇见更精彩的自己
非常感谢您的关注和支持!
登录查看更多
相关内容
专知会员服务
16+阅读 · 2019年11月30日
Arxiv
4+阅读 · 2018年5月8日