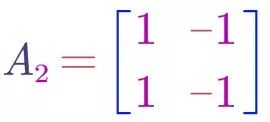如何通过心形线快速认识秩的几何意义？

本文来自公众号：超级数学建模

微信号 ：supermodeling

学好线性代数

走遍天下都不怕

在数学世界里，有许多英文名词读起来并不奇怪，但是翻译成中文就感觉莫名其妙了。比如，ideal(理想)，cohomology(上同调)，rank(秩)，等等。今天超模君就带大家来认识一下“秩”。

秩的来源

关于秩的来源，我们可追溯到19世纪后期。

1878年，德国数学家费罗贝尼乌斯(F.G.Frobenius，1849-1917)引入两矩阵等价的概念，还给出了正交矩阵的正式定义。第二年，他又在论文中提出了秩的概念：如果一个行列式的所有r+1阶子式为0，但至少有一个r阶子式不为0，那么就称r为行列式的秩(rang，德语)。只提出概念是不够的，费罗贝尼乌斯利用秩解决了矩阵可以用合同变换化成同秩的对角矩阵的问题。

F.G.Frobenius

费罗贝尼乌斯是一位很厉害的数学家，他还在椭圆函数、微分方程、数论和群论等领域有杰出贡献，以他的名字命名的数学名词和定理就有：

Frobenius自同态、Frobenius行列式定理、Frobenius公式、Frobenius群、Frobenius流形、Frobenius矩阵、Frobenius多项式、Frobenius定理、Frobenius猜想、Frobenius-Schur指标、Cauchy-Frobenius引理，等等。

费罗贝尼乌斯提出的rang，意思是等级，级别，头衔，军阶；(剧场等的)楼座，楼厅；名次。而中文的秩，本义是根据功过确定的官员俸禄，引申义为根据功过评定的官员品级，再引申义：次序、顺序。

那么为什么叫“秩”而不叫“猪”、“狗”、“猫”呢？我们来看一个情景就明白了：

每年三月份，图书馆研修室会开放给考研的学生，他们可以排队来得到一个位置。刚开始排在你前面和后面的同学互相都不认识，那么大家会按照顺序一个接着一个排队，非常有秩序。但是，随着来排队的人越来越多，他们“老乡见老乡”，我们“两眼泪汪汪”，眼睁睁看着被插队。

这时候，正常人都奋起反抗了，队伍乱成一团，到最后谁也弄不到位置。

我们来总结一下：彼此不认识，那就不相关（线性无关），就有秩序，问题就好办；反过来，彼此相关（线性相关），就没有秩序，问题就不好办。

因此，矩阵中的最大的不相关的列（行）向量的个数，就叫秩，可以理解为有秩序的程度。

当然，还有另一种猜测（纯属猜测），翻译成“秩”，应该是想表达“等级”的意思。不同矩阵的秩有大小，就好比等级的高低了。

讲得通俗一点，矩阵的秩可以理解为矩阵信息的等级划分，秩从某种程度上讲反应了矩阵内各个元素的相关性，秩越大，元素间相关性越小，每个元素代表的意义越不相似，整个矩阵蕴含的信息量就越大，反之亦然。

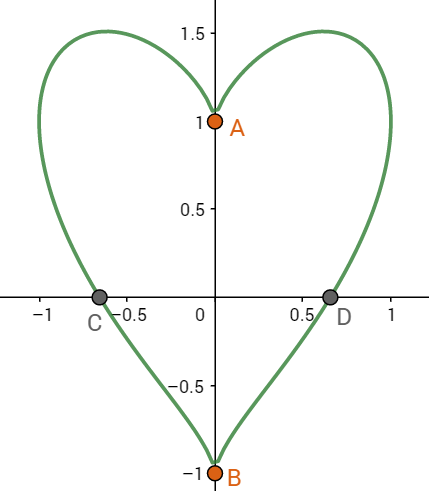
秩的几何意义

如果文字有点绕，我们通过图像来说明一下秩的几何意义吧。以心形线为栗子，标志一些特殊的点，方便等一下使用。

这不是屁股！

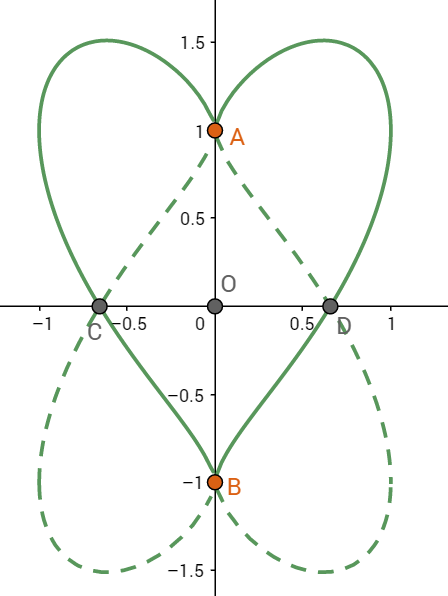
然后，我们分别以三种人为例子来讨论一下心形线的变化。第一种是最让人讨厌的颠倒是非的人，他们的心就像作了一个旋转变换，得到这样一个图形（虚线处）

其余的点同理，于是我们得到了颠倒的心形（旋转了180度），从图像很容易看出来，旋转变换后的图形依然是二维的，所以，这个旋转矩阵A1的秩就是2。

我们再来看一下第二种人。他们无论面对谁，都是一副面孔，说话一种语气，这时候他们的心就像作了一种“降维”变换，得到一条直线：

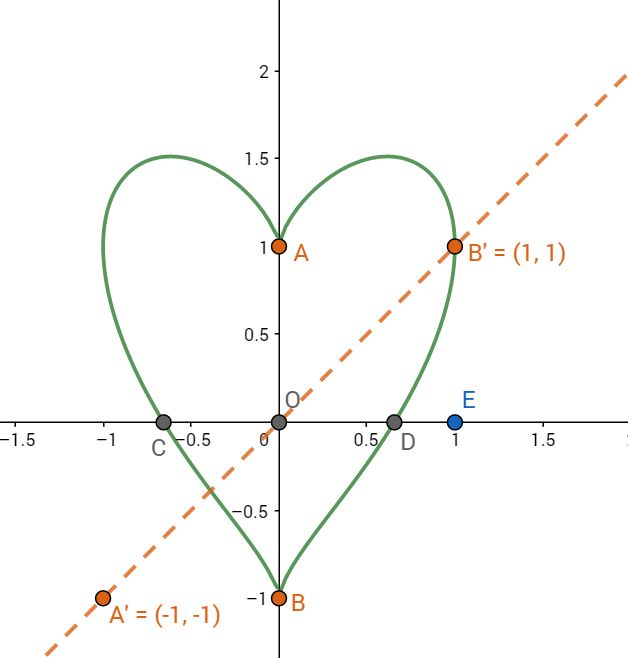
此时，变换矩阵为

可以看出，我们得到的图形（直线）是一维的，所以矩阵A2的秩就是1。

最后，我们来看一种伤感的人，他失恋了，原本轰轰烈烈的爱心一瞬间化为零，好比心形线一下子作了一个“零维”变换：

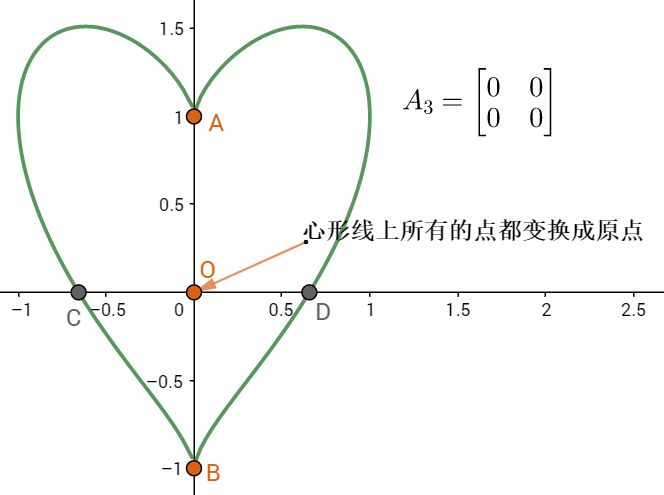
大家都知道，变换后的图形是零维的，因此变换矩阵A3的秩就是0。

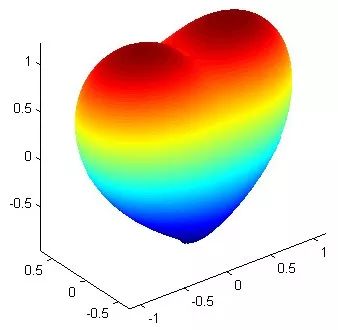
世界那么大，我们遇到的不仅仅是上面三种人。会不会有一些人，让我们的心从二维变换到三维，甚至是四维呢?

最后，我们总结一下，矩阵的秩就是列空间的维数（或列向量的极大无关组中向量的个数，这是代数版本），它的几何意义就是，一个图形（不仅仅是心形线）经过矩阵变换后，所得到的图形的维数。

秩的生活应用

最后，我们简单说一下秩的应用。

（1）计算矩阵的秩的一个实际应用是得到线性方程组的解的数量。通过判断系数矩阵和增广矩阵的秩的大小，我们可以知道线性方程组是否有解以及解的个数。可别小看方程，一个方程甚至可以改变世界。

（2）在控制理论中，矩阵的秩可以用来确定线性系统是可控的还是可观察的。

（3）在通信复杂性领域，函数的通信矩阵的秩给出了双方计算函数所需的通信量的界限。

（4）在找工作中，我们尽量选择“满秩”公司，为什么呢？留给小伙伴们思考（可结合相关性与秩的关系来考虑）。

编辑：雾里熊

---

近期热门文章Top10

↓ 点击标题即可查看 ↓

1. 人类一思考，上帝就要忙疯掉……

2. 原来，这些我们都默认科学家早已解决了的问题，至今仍然无解

3. 理工科学霸的子女更易患自闭症

4. 鸡蛋从高空坠落能砸死人，为什么猫却摔不死？科学告诉你答案

5. 光学3分钟：从入门到放弃

6. 光速为什么如此重要？

7. 量子计算陷入难解困境，未来发展何去何从？

8. 除了《时间简史》，关于霍金你还应该知道这些！

9. 速速收藏！可乐竟然还有这些神奇的用途！

10. 石墨烯研究的意外发现，是否能解开高温超导之谜

点此查看以往全部热门文章

---