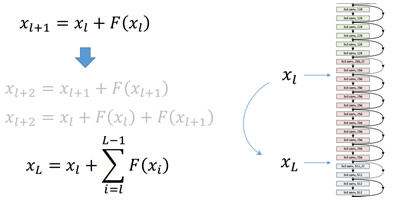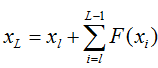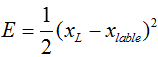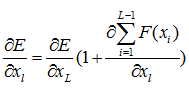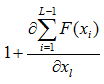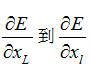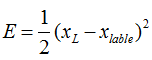变种神经网络的典型代表：深度残差网络

2017 年 10 月 20 日 机器学习研究会

随着人们对于神经网络技术的不断研究和尝试，每年都会诞生很多新的网络结构或模型。这些模型大都有着经典神经网络的特点，但是又会有所变化。你说它们是杂交也好，是变种也罢，总之对于神经网络创新的各种办法那真叫大开脑洞。

而这些变化通常影响的都是使得这些网络在某些分支领域或者场景下的表现更为出色（虽然我们期望网络的泛化性能够在所有的领域都有好的表现吧）。深度残差网络（Deep Residual Network）就是众多变种中的一个代表，而且在某些领域确实效果不错，例如目标检测（Object Detection）。

应用场景

对于传统的深度学习网络应用来说，我们都有这样一种体会，那就是网络越深所能学到的东西就越多。当然收敛速度同时也就越慢，训练时间越长，然而深度到了一定程度之后就会发现有一些越往深学习率越低的情况。深度残差网络的设计就是为了克服这种由于网络深度加深而产生的学习率变低，准确率无法有效提升的问题，也称作网络的退化问题。甚至在一些场景下，网络层数的增加反而会降低正确率。

关于深度残差网络的介绍资料不算多，至少比起传统的BP、CNN、RNN网络的介绍资料就少得多了，我这边参考的是何恺明先生在网上公开的一个介绍性资料“Deep Residual Networks——Deep Learning Gets Way Deeper”。

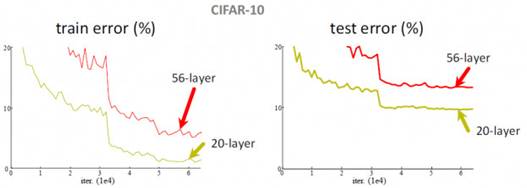
说到对比传统的卷积神经网络在做分类器的时候，在加深网络层数的过程中是会观察到一些出出乎意料的现象的。例如在CIFAR-10项目上使用56层的3×3卷积核的网络其错误率无论是训练集上还是验证集上，都高于20层的卷积网络，这就尴尬了。通常为了让网络学到更多的东西，是可以通过加深网络的层数，让网络具备更高的VC维这样的手段来实现的。但眼前的事实就是这样，加到56层的时候其识别错误率是要比在20层的时候更加糟糕。

这种现象的本质问题是由于出现了信息丢失而产生的过拟合问题。这些图片在经过多层卷积的采样后在较深的网络层上会出现一些奇怪的现象，就是明明是不同的图片类别，但是却产生了看上去比较近似的对网络的刺激效果。这种差距的减小也就使得最后的分类效果不会太理想，所以解决思路应该是尝试着使它们的引入这些刺激的差异性和解决泛化能力为主。所以才会考虑较大尺度地改变传统CNN网络的结构，而结果也没有让我们失望，新型的深度残差网络在图像处理方面表现出来的优秀特性确实令我们眼前一亮。

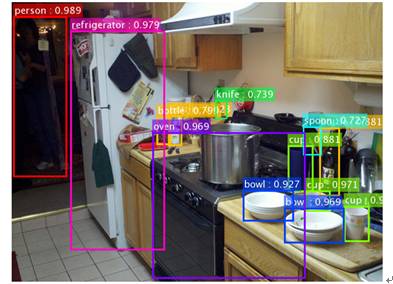
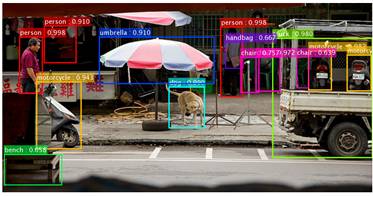
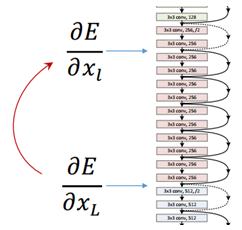
到目前为止，在图像分类（Image Classification）、对象检测（Object Detection）、语义分割（Semantic Segmentation）等领域的应用中，深度残差网络都表现出了良好的效果。上面这几张图都是尝试用深度残差网络在一张图片中去识别具体的一个目标，每个目标的属性标注是基于微软的COCO数据集的数据标识。物品（人）的框图上还标注了一个小数，这个数字就是概率（或者称确信度Precision），指模型识别这个物体种类的确信度。我们能看到，在这个图片中大部分物体的识别还是非常准确的。

结构解释与数学推导

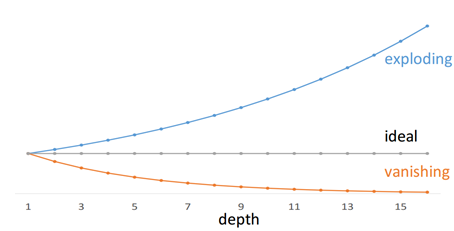
深度网络有个巨大的问题，那就是随着深度的加深，很容易出现梯度弥散和梯度爆炸的问题。

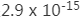
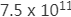
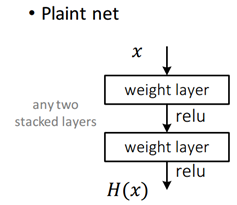
前面我们也提过这个问题，因为网络深度太大所以残差传播的过程在层与层之间求导的过程中会进行相乘叠加，一个小于1或一个大于1的数字在经过150层的指数叠加就会变得很大或者很小，我们自己手算一下也能算出来，0.8的150次方大约是，1.2的150次方大约是，这两种情况都是极为严重的灾难，任何一种都会导致训练劳而无功。

在传统的平网络（Plain Network）中，一层的网络的数据来源只能是前一层网络，就像上图这样，数据一层一层向下流。对于卷积神经网络来说，每一层在通过卷积核后都会产生一种类似有损压缩的效果，可想而知在有损压缩到一定程度以后，分不清楚原本清晰可辨的两张照片并不是什么意外的事情。这种行为叫有损压缩其实并不合适，实际在工程上我们称之为降采样（Downsampling）——就是在向量通过网络的过程中经过一些滤波器（filters）的处理，产生的效果就是让输入向量在通过降采样处理后具有更小的尺寸，在卷积网络中常见的就是卷积层和池化层，这两者都可以充当降采样的功能属性。主要目的是为了避免过拟合，以及有一定的减少运算量的副作用。在深度残差网络中，结构出现了比较明显的变化。

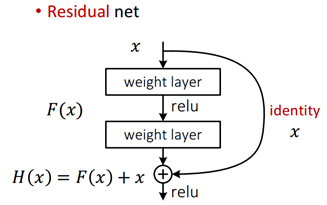
在这种情况下，会引入这种类似“短路”式的设计，将前若干层的数据输出直接跳过多层而引入到后面数据层的输入部分，如图所示。这会产生什么效果呢？简单说就是前面层的较为“清晰”一些的向量数据会和后面被进一步“有损压缩”过的数据共同作为后面的数据输入。而对比之前没有加过这个“短路”设计的平网络来说，缺少这部分数据的参考，本身是一种信息缺失丢失的现象本质。本来一个由2层网络组成的映射关系我们可以称之为F(x)的这样一个期望函数来拟合，而现在我们期望用H(x)=F(x)+x来拟合，这本身就引入了更为丰富的参考信息或者说更为丰富的维度（特征值）。这样网络就可以学到更为丰富的内容。

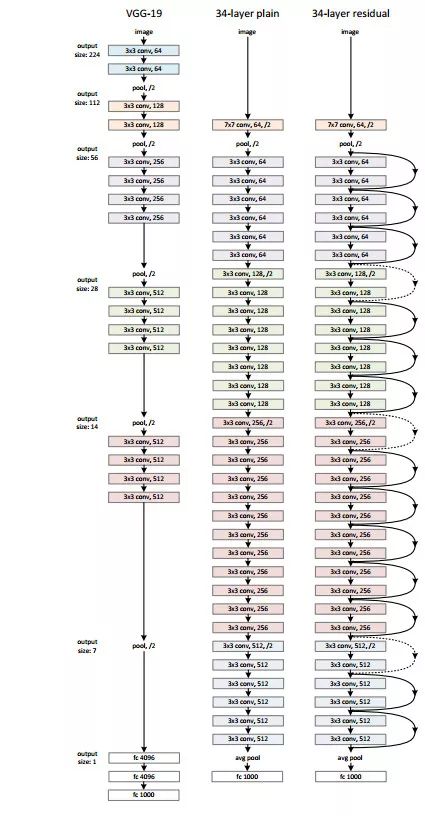
这张图比较了三种网络的深度和结构特点，VGG-19、34层的“平网络”——也就是普通34层的CNN网络，还有34层的深度残差网络。

在深度残差网络的设计中通常都是一种“力求简洁”的设计方式，只是单纯加深网络，所有的卷积层几乎都采用3×3的卷积核，而且绝不在隐藏层中设计任何的全连接层，也不会在训练的过程中考虑使用任何的DropOut机制。以2015年的ILSVRC & COCO Copetitions为例，以分类为目的深度残差网络“ImageNet Classfication”居然能够达到152层之深，也算是破了纪录了。

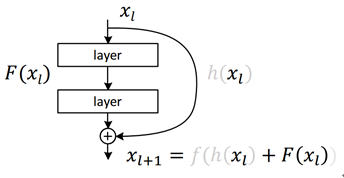
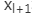
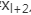
这种短路层引入后会有一种有趣的现象，就是会产生一个非常平滑的正向传递过程。我们看和其前面一层xl的关系是纯粹一个线性叠加的关系。如果进一步推导及其以后层的输出会发现展开后是这样一个表达式：

也就是后面的任何一层xL向量的内容会有一部分由其前面的某一层xl线性贡献。

好，现在看反向的残差传递，也是一个非常平滑的过程。这是刚才我们看到的某层输出xL的函数表达式

那么残差我们定义为E（就是Loss），应该有

后面的xlable表示的是在当前样本和标签给定情况下某一层xL所对应的理想向量值，这个残差就来表示它就可以了。下面又是老生常谈的求导过程了，这里就是用链式法则可以直接求出来的，很简单

注意这个地方，用白话解释一下就是任意一层上的输出xL所产生的残差可以传递回其前面的任意一层的xl上，这个传递的过程是非常“快”或者说“直接”的，那么它在层数变多的时候也不会出现明显的效率问题。而且还有一个值得注意的地方，后面这项

它可以使得

是一个线性叠加的过程而非连乘，所以它自然也不太可能出现梯度消失现象。这些就是从数学推导层面来解释为什么深度残差网络的深度可以允许那么深，并且还没有出现令人恐惧的梯度消失问题和训练效率问题。

补充说明一下，

中的E和xL在这里泛指某两个不同层之间的关系，指代他们的残差和输出值。大家请注意，在一个多层的网络中，每一层我们都可以认为是一种分类器模型，只不过每一层分类器的具体分类含义人类很难找到确切的并且令人信服的物理解释。然而每一层的各种神经元在客观上确实充当着分类器的功能，它将前面一层输入的向量进行采样并映射为新的向量空间分布。所以从这个角度去解释的话，