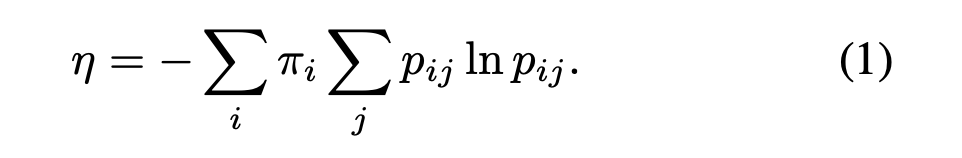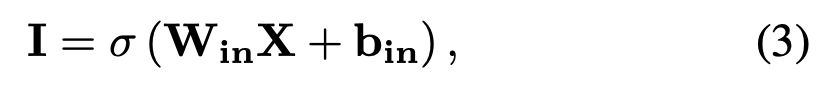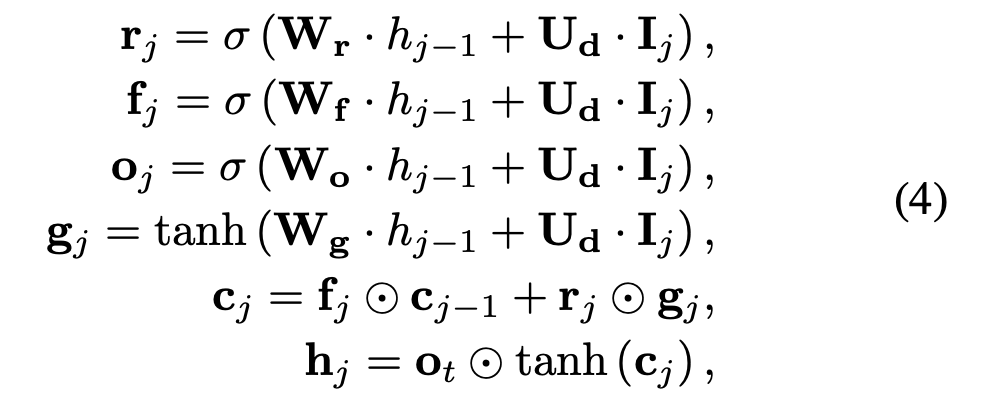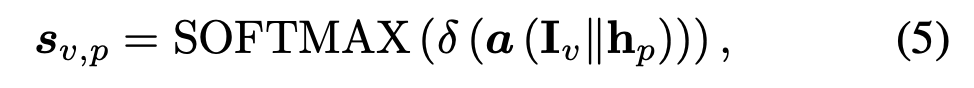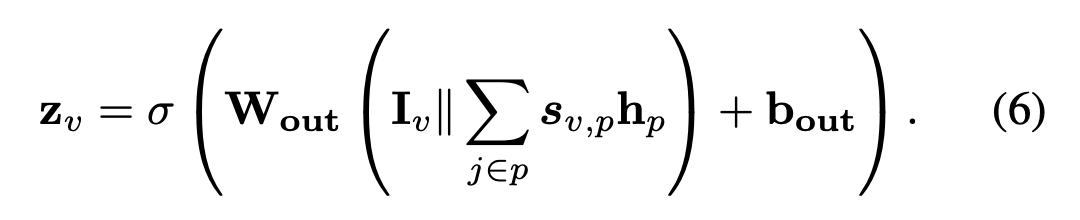IJCAI 2022 | 超越同质性的图神经网络

会员服务 ·

IJCAI 2022 | 超越同质性的图神经网络

2022 年 9 月 6 日 PaperWeekly

©作者 | 焦子豪

单位 | 南京邮电大学

来源 | MIND Laboratory

论文标题：

Beyond Homophily: Structure-aware Path Aggregation Graph Neural Network

收录会议：

IJCAI 2022

论文来源：

http://yangy.org/works/gnn/IJCAI22_Beyond.pdf

论文介绍

图神经网络 (GNNs) 已经在许多现实世界任务中得到了广泛研究与应用。然而，GNN 基于同质性的假设限制了其在异质图上的表示学习能力。本文聚焦于图上的路径，用来表示丰富的语义和结构信息。本文提出了路径聚合图神经网络 Path Aggregation Graph Neural Network (PathNet)，旨在将 GNN 同时推广到同质图和异质图上。

论文动机

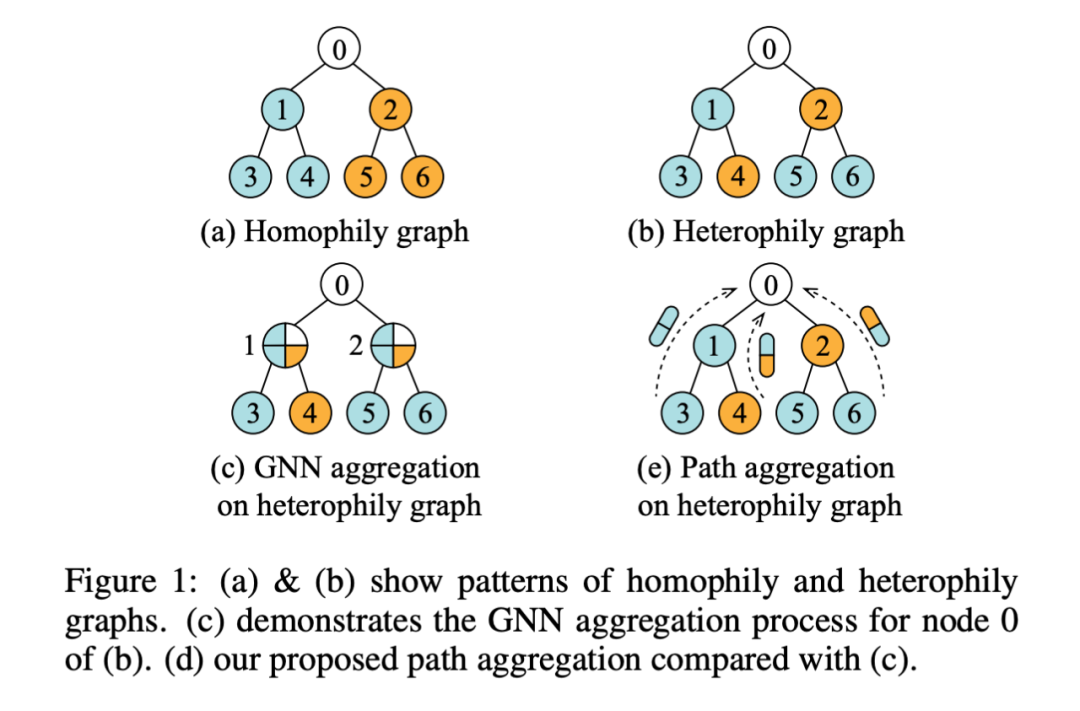
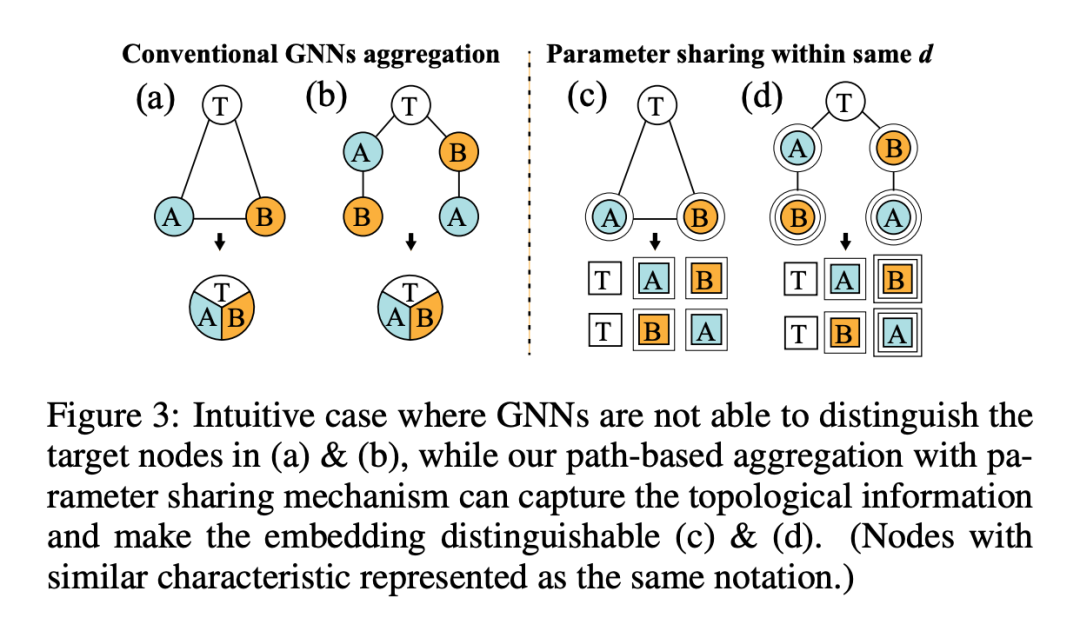
尽管 GNN 在大多数任务上取得了良好的结果，大部分 GNN 是基于同质性的条件设计出来的。也就是说，相连接的结点对倾向于拥有相似的特征，或属于同种类别（“birds of a feather flock together”）。然而，现实世界中有很多图并不具有同质性，表现出“异性相吸”的特点。

如图所示，a 和 b 分别表示的是同质图和异质图。在异质图中，相邻的结点可能拥有不同的特征，或属于不同的类别。如 c 所示，在异质图 b 中，要生成结点 0 的表示，需要首先对结点 1 和 2 的表示进行学习。

对于结点 1，聚合其周围邻居 0、3、4，对于结点 2，聚合其周围邻居 0、5、6。会发现结点 1 和 2 聚合以后的特征是同样的：

这对于结点 0 来说是无法区分的。然而结点 1 和 2 的原始特征是不同的，这表明 GNN 聚合操作对于异质图的缺陷性。

然而本文提出的图上的路径模式能够很好的对同质图和异质图进行建模。如图 d，本文提出的方法聚合了三种路径，分别通过结点 1、3；1、4；2、5/6 生成。

本文的贡献概括如下：

1. 提出了路径聚合模式，用于捕获同/异质图的结构信息；

2. 设计了 end-to-end 模型 PathNet，对路径的次序和距离信息进行编码，以获得丰富的语义信息；

3. 实验结果表明本文的方法在异质图上取得了 SOTA 的结果，在同质图上取得了 competitive 的结果。

PathNet

3.1 Maximal Entropy Path Sampler

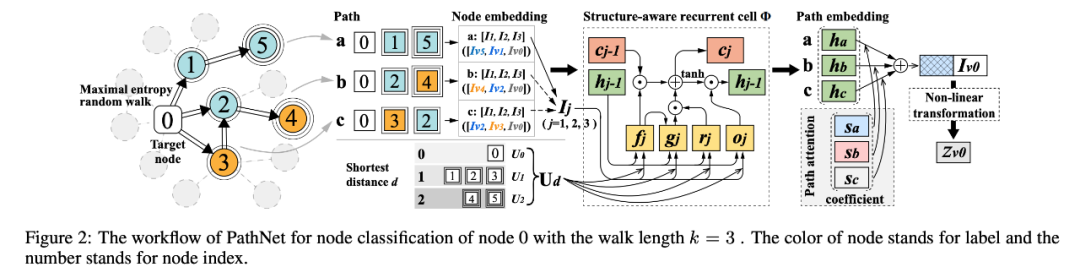
有别于传统的随机游走，本文采取基于最大熵的随机游走，对路径进行采样。这样的随机游走每一步保持熵增，同时引入向量中间性作为衡量结点重要程度的指标：

其中，是随机游走的最大熵，是平稳分布。

3.2 Structure-aware Path Aggregator

本文设计了一个路径聚合器，用于聚合路径信息。同时设计了一个循环单元，对路径嵌入编码，以结合路径中各结点的次序和距离信息。

如图所示，本文采取的路径聚合策略能够弥补传统 GNN 面对异质图的无力。与传统的各自对各层的结点进行聚合不同，本文提出了循环单元，对路径序列进行编码，以保留每个结点的次序信息：

其中是所有结点的特征，是结点嵌入，和是可学习的参数，是激活函数。

本文设计循环单元为：

其中表示结点 v 在路径第 j 步的潜在嵌入。分别表示输入、遗忘、输出门。

本文为每个结点设计了路径偏好 (path preference)，即学习不同路径对于目标结点聚合的重要性。本文计算偏好系数如下：

其中是可训练的权重参数，是经式 4 计算得出的路径 p 的嵌入，是目标结点的嵌入。 LeakvReLU。

最后将偏好系数作为路径权重，对结点 v 进行预测：

实验

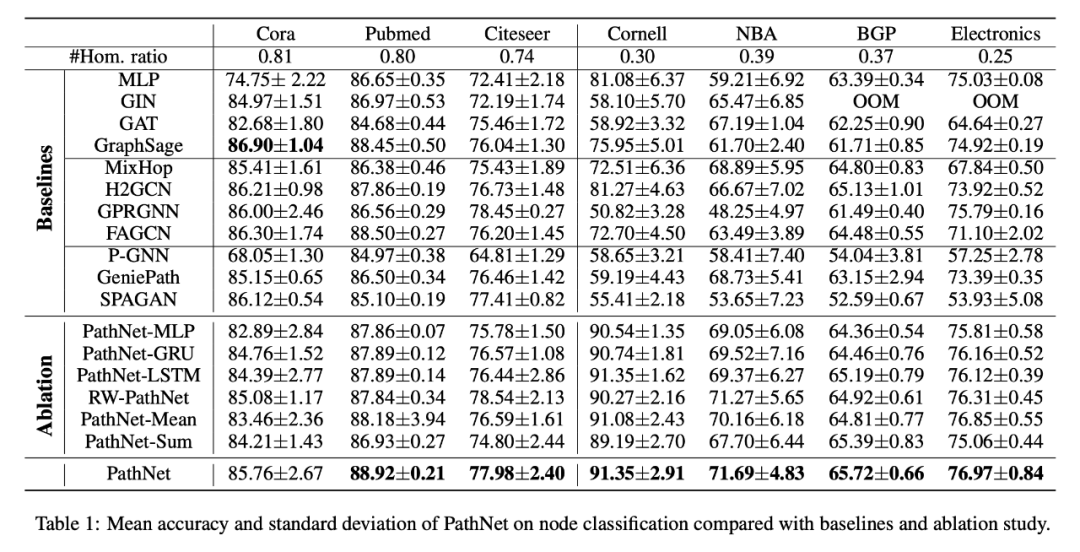
本文采取了 7 个真实世界数据集：3 个同质（绿色）& 4 个异质（黄色）。可以看出 PathNet 在所有的异质图数据集上均取得了 SOTA 的结果，在同质图数据集上也有优越的性能。

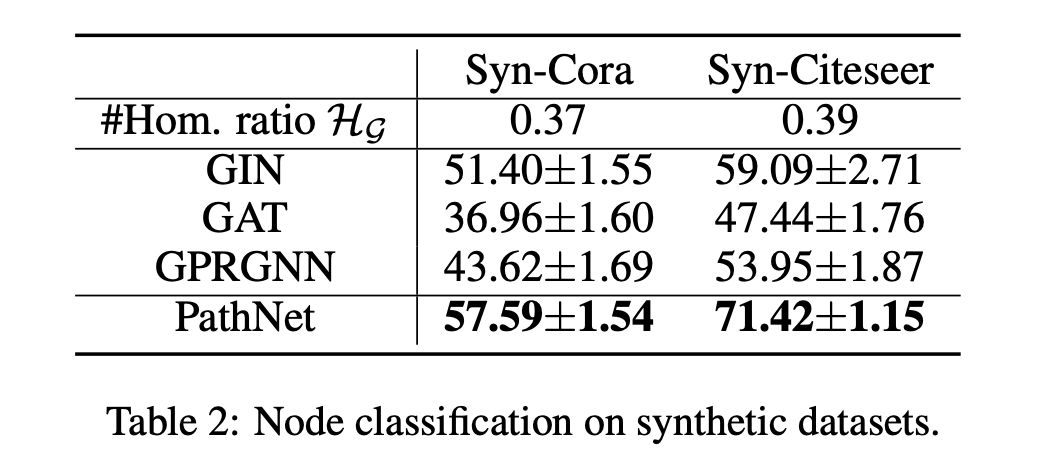
在人工数据集上取得了 SOTA 的结果。

总结

本文提出了采用路径对图中结点进行聚合的方法 PathNet，能够同时捕获同/异质图中的语义和结构信息。首先采用最大化熵对路径进行采样；接着采用循环单元对每条路径进行基于结构的聚合；然后对路径偏好进行处理。作为 end-to-end 的模型，PathNet 在同质图和异质图上均取得了 SOTA 的结果。

更多阅读