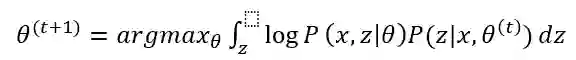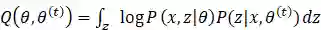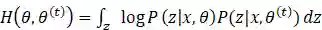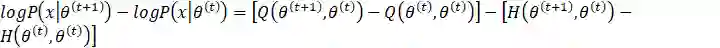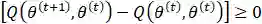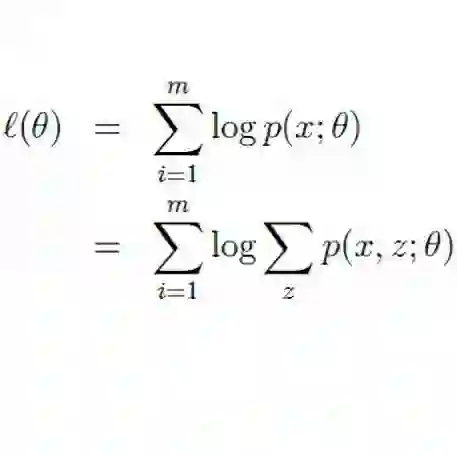五分钟快速了解EM算法

点击上方，选择星标或置顶，每天给你送干货 ！

阅读大概需要8分钟

跟随小博主，每天进步一丢丢

每日英文

There is a wholeness about the person who has come to terms with his limitations.

人生的完整在于一个人知道如何面对他的缺陷。

Recommender：云不见

作者：刘子仪

编辑：王萌 (深度学习自然语言处理公众号)

EM算法是机器学习中比较重要的用于对于带有隐变量的联合概率模型参数进行极大似然估计的方法。因为这篇文章单独把EM算法抽出来讲，对于没有统计学习基础的同学来说，理解这个算法是如何引出的可能会有些困难，会需要关于ELBO，KL散度等相关知识储备。所以本文将从以下几个方面来讲解，让入门的同学可以快速对EM算法有一个大体的认知：

• EM算法要解决什么问题

• EM算法的E-step和M-step以及证明其收敛性

• EM算法的应用

一.EM算法要解决什么问题

EM（期望最大化）算法于1976年提出，这篇论文的名字是“Maximum Likelihood for Incomplete Data via the EM Algorithm”。其实论文题目已经非常清楚地说明了EM算法作用——从incomplete data中进行极大似然求解。

什么是incomplete data呢，作者给出的定义是如果有两个样本空间Z和X以及关于Z->X的映射。x∈X是可以观察到的数据，而z∈Z是不能直接观察到，只能通过x间接观察到的数据，这样的数据就是incomplete data，我们称z为隐变量，EM算法的目的就是通过E-step和M-step迭代的方式进行极大似然估计，对含有隐变量的概率模型进行参数估计。

二.EM算法的公式以及证明其收敛性

假设输入的数据是观测数据X，隐变量数据Z，联合分布为P(x,z|θ)，条件分布P(z|x,θ)，要求解的是模型参数θ。

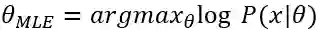MLE（极大似然估计）问题的其实就是求解 ，为了方便求解一般会加上log，后面这个式子也称为log likelihood。 EM算法就是通过迭代的方式求出这个式子的解析解。

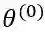首先选择参数初值 , 开始迭代。 假设 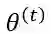是第t次迭代参数的估计值，在第t+1次迭代时，EM算法的公式是 

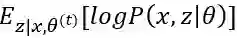
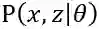
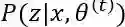
这个式子后半部分的积分其实就是求期望，对应的E步我们称这个函数为Q函数，在证明收敛性时会用到，前面的加上argmax函数就是最大化，对应M步。式中是联合概率，是后验概率。

需要注意的是，虽然参数的初值可以任意选择，但是EM算法对于初值是敏感的，随意取初值很有可能得不到好的结果，所以还是要慎重取值。

了解了公式之后，接下来我们来证明EM算法的收敛性。即证明

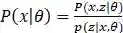 首先 ，两边同时取对数得 

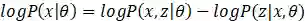
由上文可知 

令 

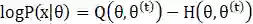
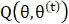
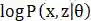
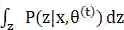
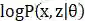
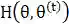
则 （解释说明：对于来说，和求期望没有关系，可以提取出来，而后面的等于1，所以等于，同理。

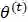
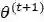
对于上式分别取θ为和并相减，有

为了证明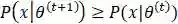，只需证明上式右端为非负的。由于在EM算法里，在M步会对Q函数求极大，则 

对于第二项

   

= 

= 

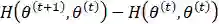
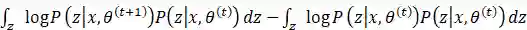
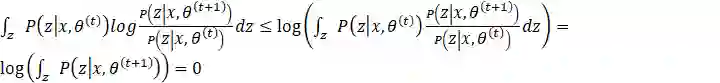
这里的不等式由Jenson不等式得到。其实如果了解KL散度可以发现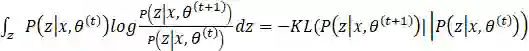  又因为KL散度大于等于0，所以可得最后结果小于等于0。

三.EM算法的应用

之前有一次面试，面试官问我机器学习算法都会哪些，我说到了EM算法，然后她问EM算法有什么应用吗，她觉着EM算法没有什么应用场景。其实EM算法应用还是比较广泛的，尤其是在高斯混合模型做参数估计的时候。EM算法不像感知机，支持向量机应用普遍，它很少作为分类算法被使用，EM算法作为一种参数估计的方法，更多是和概率模型结合使用，例如用于马尔可夫模型参数求解。同时EM算法还有一些推广：GEM算法，变分EM等等。

说个正事哈

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方“深度学习自然语言处理”，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

投稿或交流学习，备注：昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多：机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦

推荐两个专辑给大家：

专辑 | 李宏毅人类语言处理2020笔记

专辑 | NLP论文解读

整理不易，还望给个在看！