会员服务 ·

计算机视觉面试复习笔记：深度学习基础-神经网络

2021 年 10 月 18 日 极市平台

↑ 点击蓝字关注极市平台

作者丨南山

来源丨AI约读社

编辑丨极市平台

极市导读

计算机视觉考查的面试知识点进行总结，学习、记录、分享和复习。 >>加入极市CV技术交流群，走在计算机视觉的最前沿

笔记目录：

深度学习基础

神经网络：神经网络的组成、损失函数，梯度下降，神经网络的反向传播，激活函数
卷积神经网络：卷积，全连接层，池化层，卷积层，反卷积层，BatchNormalization，感受野计算
深度学习基础面试常见问题总结

计算机视觉（三大基础任务）

图像分类：VGG、GoogleNet、ResNet、SENet、Mobilenet系列
目标检测：FastRCNN、YOLO、SSD、CenterNet、Detr、DetectoRS、EffiectDet
图像分割：U-Net、FastFCN、DeepLab、MaskRCNN、SETR

部分计算机视觉细化领域

数据扩增和半监督学习
人脸检测和活体检测
图像篡改检测
OCR字符识别
NAS网络结构自动搜索
视觉室内定位

由于作者水平有限可能会存在遗漏和错误的情况欢迎大家指正，由于篇幅有限，本文会分成多篇文章发出~

一、神经网络

本节我们将梳理神经网络的几个重要部分内容的知识点，首先是神经网络的组成，损失函数、梯度下降法、梯度的反向传播，L1和L2正则化

1.1 神经网络的组成

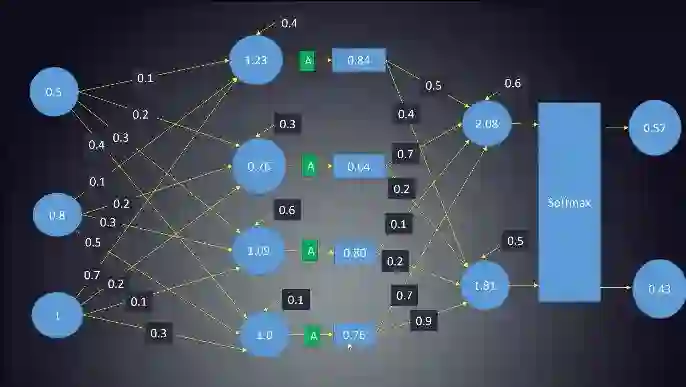
如上图简单的前馈神经网络所示，神经网络主要架构是由神经元、层和网络三个部分组成。整个神经网络包含一系列基本的神经元、通过权重相互连接。神经元是神经网络最基本的单元。

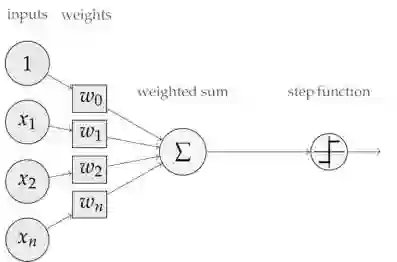
神经元：神经元是包含权重和偏置项的函数，等待数据传递给它们。接收数据后，它们执行一些计算，然后使用激活函数将数据限制在一个范围内

其中的W就是权重，我们需要神经网络通过训练学习到合适的权重，学习的方法一般是通过计算损失函数然后利用梯度下降法来更新权重
激活函数：神经元经过加权融合后一般还需要经过激活函数激活，主要作用就是为了增加神经网络模型的非线性。否则你想想，没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。主要的激活函数有sigmoid、tanh、ReLU等。

Sigmoid函数：

这里要对神经网络的一些基本的部分进行说明。

输入层，即输入x的那一层。
输出层，即输出y的那一层，如果是分类任务可以加上softmax层计算每个类别的概率。
隐层，输入层和输出层之间不管隔了多少层都叫隐层。

1.2 损失函数 Loss Function

损失函数的作用：机器学习算法的设计使其可以从错误中“学习”并使用我们提供给他们的训练数据来“更新”神经元的权重。但是他们如何量化这些错误呢？这是通过使用“损失函数”来完成的，该函数可以帮助算法了解与基本事实相比，其预测的错误程度。选择合适的损失函数很重要，因为它会影响算法尽快生成最佳结果的能力。

L2 LOSS

这是可用的最基本的损失，也称为MSE Loss。这依赖于两个向量[预测和真实标签]之间的欧式距离。简单来说就是预测值和真实值的平方差。
L2 Loss 对异常值非常敏感，因为误差是平方的。
一般用于回归任务，如回归目标检测中的box

CROSS-ENTROPY LOSS(交叉熵损失函数)

Cross Entropy Loss Function交叉熵损失函数是使用对数（loge）的更高级的损失函数。与L2 Loss 相比，这有助于加快对神经网络的训练。
在二分类的情况下交叉熵损失函数被称为 Loss, 模型最后需要预测的结果只有两种情况, 对于每个类别我们的预测得到的概率为和。

此时表达式为：

其中：

一一表示样本i的label，正类为1，负类为0
一一表示样本i预测为正的概率

1.3 梯度下降法

在神经网络中，不论是哪种网络，最后都是在找层和层之间的关系(参数，也就是层和层之间的权重)，而找参数的过程就称为学习，所以神经网路的目的就是不断的更新参数，去最小化损失函数的值，然后找到最佳解。选择合适的梯度下降优化方法可以让我们取得更好的结果，接下来我们简单的梳理梯度下降的优化算法。

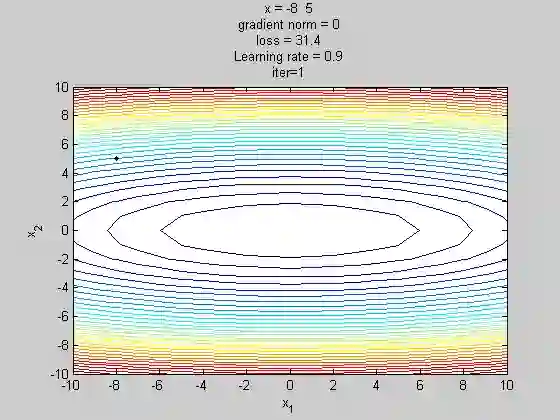
梯度下降法(gradient descent，GD)

梯度下降法(gradient descent)是最佳化理论里面的一个一阶找最佳解的一种方法，主要是希望用梯度下降法找到函数的局部最小值，因为梯度的方向是走向局部最大的方向，所以在梯度下降法中是往梯度的反方向走。

简单来说梯度下降法（Gradient Descent Algorithm，GD）是以负梯度方向求解损失函数J(θ) 的全局最小值的一种迭代方法。

梯度公式如下：

这边的是参数, 是学习率(Learning rate)。找「解」的时候公式是往梯度的反方向更新, 但一次要更新多少, 就是由学习率来控制的。

GD的缺点：1、每更新一次参数，就要遍历全部数据集，计算起来非常慢。2、容易陷入极小值点，因为在极小值点（鞍点）梯度为0，所以参数不会更新。

随机梯度下降法(Stochastic gradient descent, SGD)

我们一般看深度学习的介绍，最常看到的梯度下降优化算法是「随机梯度下降法(Stochastic gradient descent, SGD)」(这篇我为了缩短篇幅，Mini-batch SGD我们把它归纳到SGD内)，我们简单说一下这个跟梯度下降GD的差别。

在更新参数的时候

GD我们是一次用全部训练集的数据去计算损失函数的梯度就更新一次参数。

SGD就是一次跑一个样本或是小批次(mini-batch)样本然后算出一次梯度或是小批次梯度的平均后就更新一次，那这个样本或是小批次的样本是随机抽取的，所以才会称为随机梯度下降法。

SGD的缺点： SGD每次的更新并不是向着整体最优化方向，虽然速度快，准确度下降，并不是全局最优。SGD 在收敛时浮动，不稳定，在最优解附近波动，难以判断是否已经收敛。

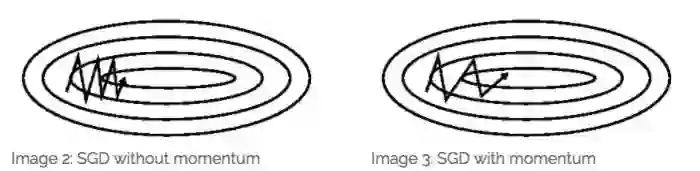
Momentum

为了缓解SGD的在收敛时由于学习率过大导致在最优解附近波动的问题，Momentum在计算梯度时，当前时刻的梯度是从开始时刻到当前时刻的梯度指数加权平均

其中m是momentum项(一般设定为0.9)。主要是用在计算参数更新方向前会考虑前一次参数更新的方向，如果当下梯度方向和历史参数更新的方向一致，则会增强这个方向的梯度，反之，则梯度会衰退。然后每一次对梯度作方向微调。这样可以增加学习上的稳定性(梯度不更新太快)，这样可以学习的更快，并且有摆脱局部最佳解的能力。如下图所示：

Adam

上面的算法中的学习率都是固定不变的，Adam是对学习率自适应调整。Adam不仅和momentum一样计算参数更新方向前会考虑前一次参数更新的方向，还在学习率上依据梯度的大小对学习率进行加强或是衰减。

m t和v t分别是梯度的一阶动差函数和二阶动差函数(非去中心化)。因为m t和v t初始设定是全为0的向量，Adam的作者发现算法偏量很容易区近于0，因此他们提出修正项，去消除这些偏量。

1.4 神经网络的反向传播

从上文我们了解到了，在神经网络参数更新的时候通过计算损失函数对各参数的梯度利用梯度下降法来更新参数，那么怎么计算各参数的梯度呢？这就需要利用的神经网络的反向传播了。

神经网络的训练过程中，反向传播通过导数链式法则计算损失函数对各参数的梯度，并根据梯度进行参数的更新。 损失对参数梯度的反向传播可以被这样直观解释：由A到传播B，即由得到，由导数链式法则实现。所以神经网络的BP就是通过链式法则求出对所有参数梯度的过程。

1.5 激活函数

激活函数增加了神经网络模型的非线性，解决线性模型所不能解决的问题。下面我们介绍几个常用的激活函数:sigmoid、tanh、ReLu、Leaky ReLU。

sigmoid

sigmoid函数：

sigmoid导数：

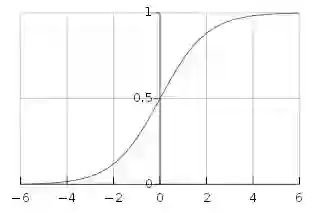
sigmoid图像：

从上图可以知道sigmoid的输出范围是（0，1），因此它对每个神经元的输出进行了归一化；对于机器学习和数据科学初学者来说，它是最常用的激活函数之一。但是对于高级神经网络，由于各种缺点（梯度消失问题），Sigmoid 函数不是首选。

Sigmoid的缺点：存在梯度消失和爆炸问题，虽然 sigmoid 函数及其导数很简单，有助于减少制作模型所需的时间，但由于导数的范围很小，因此存在信息丢失的主要缺点。

梯度消失： 当我们的神经网络越深，信息在每一层被压缩和丢失的情况就越多，这在每一步都会放大，并导致总体上的主要数据丢失。

梯度爆炸： 对于 sigmoid 函数，因为它的输出是正的，我们所有的输出神经元也都有正输出，随着网络层数加深容易出现梯度爆炸的现象。

Tanh 双曲正切激活函数

函数：

导数：

tanh图像：

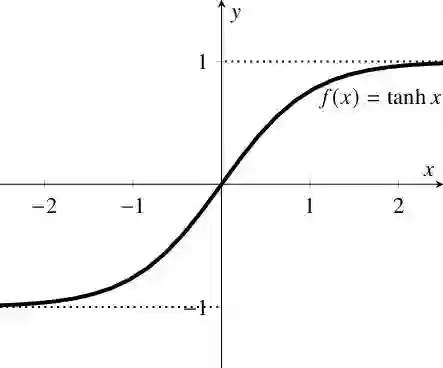
在tanh函数中，我们在 sigmoid 函数中看到的缺点得到了解决（不完全），这里与 sigmoid 函数的唯一区别是曲线在原点上是对称的，值范围从 -1 到 1。
ReLU (Rectified Linear Units)

ReLU函数：

ReLU导数：

ReLU图像：

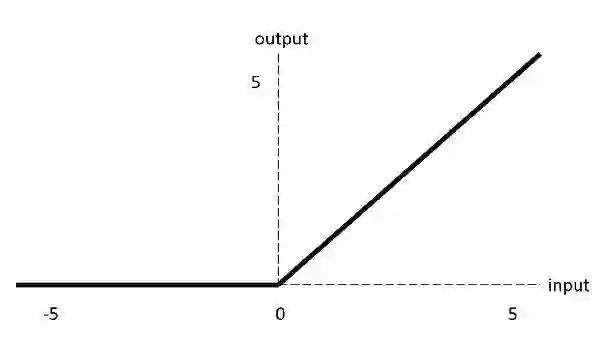
ReLU如果输入小于 0，则输出为 0，否则为原始输出。也就是说，如果输入大于0，则输出等于输入。ReLU 的操作更接近于我们生物神经元的工作方式。现在大多数深度学习都使用ReLU代替Sigmoid激活函数用于计算机视觉、语音识别、自然语言处理和深度神经网络等。与 tanh 或 sigmoid 函数相比，ReLU 在具有更快的收敛速度。

RELU的优点：

稀疏激活：在随机初始化的网络中，只有大约 50% 的隐藏单元被激活（具有非零输出）。
更好的梯度传播：与在两个方向上都有限制的 sigmoid，tanh激活函数相比，缓解了梯度消失问题。
高效计算：只有比较、加法和乘法，运算速度更快。
尺度不变：max ( 0, ax ) = a max ( 0 , x ) a ≥ 0

ReLU 的缺点：

当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。但是在反向传播过程中，如果输入负数，则梯度将完全为零有可能导致神经元死亡，也就是流经神经元的梯度从这一点开始将永远是0，出现权重无法更新的情况。

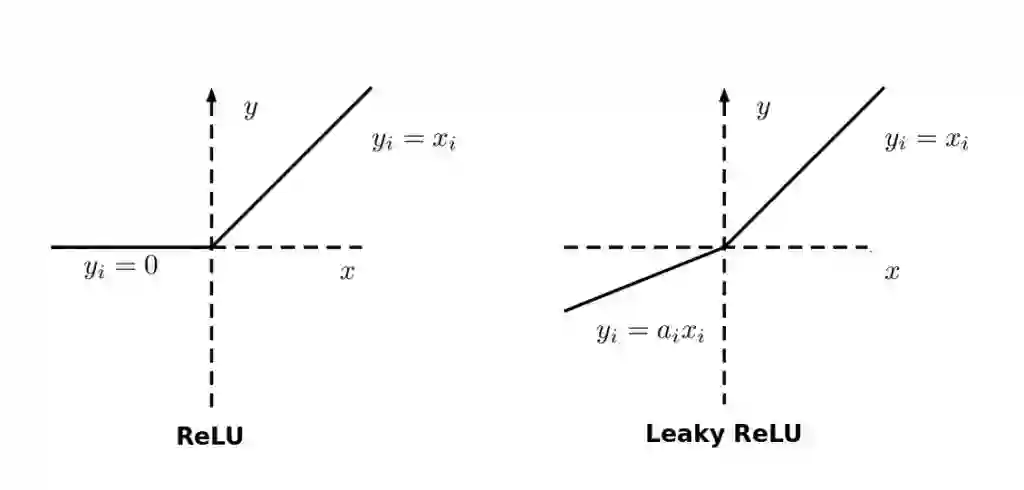
Leaky ReLU

如果神经网络中存在大量死亡神经元，则其性能是受到影响，这可以通过使用所谓的Leaky ReLU来纠正，其中Leaky ReLU的斜率 x=0 的左侧发生变化，从而扩展ReLU的范围。

Leaky ReLU函数： ,如当

Leaky ReLU导数:

Leaky ReLU图像：

神经网络的深度和宽度

神经网络的深度决定了网络的表达能力，早期的backbone设计都是直接堆叠卷积层，它的深度指的是神经网络的层数；后来的backbone设计采用了更高效的module（或block）堆叠的方式，每个module是由多个卷积层组成，这时深度指的是module的个数。

神经网络的宽度决定了网络在某一层学习到的信息量，指的是卷积神经网络中最大的通道数，由卷积核数量最多的层决定。通常的结构设计中卷积核的数量随着层数越来越多的，直到最后一层feature map达到最大，这是因为越到深层，feature map的分辨率越小，所包含的信息越高级，所以需要更多的卷积核来进行学习。通道越多效果越好，但带来的计算量也会大大增加，所以具体设定也是一个调参的过程，并且各层通道数会按照8×的倍数来确定，这样有利于GPU的并行计算。